Representing non-double-couple centroid moment tensors
The full centroid moment tensor solution for an earthquake (the so-called Harvard/LDEO CMT) may include a non-double-couple element, especially where seismicity is associated with magmatism, hydrothermal activity, or landslip (Jullian et al. 1998, Miller et al. 1998, Yunga et al. 2005). The solution is then represented graphically (Figure 11a) by the intersection of the moment tensor’s eigen-ellipsoid with a concentric focal sphere.
Figure 11a. Basketball models

Non double couple Centroid Moment Tensor (CMT) solution yields a “basket ball” model. Model created by intersecting a bi-cone of elliptical base with a concentric sphere.
Figure 11b. Pool ball model

Special case of a CMT with a spheroidal eigen-ellipsoid yields a small circle (“pool ball”) model. This model is generated by intersecting a sphere with a bi-cone of circular base.
Figure 11c. CMT eigen-ellipsoid
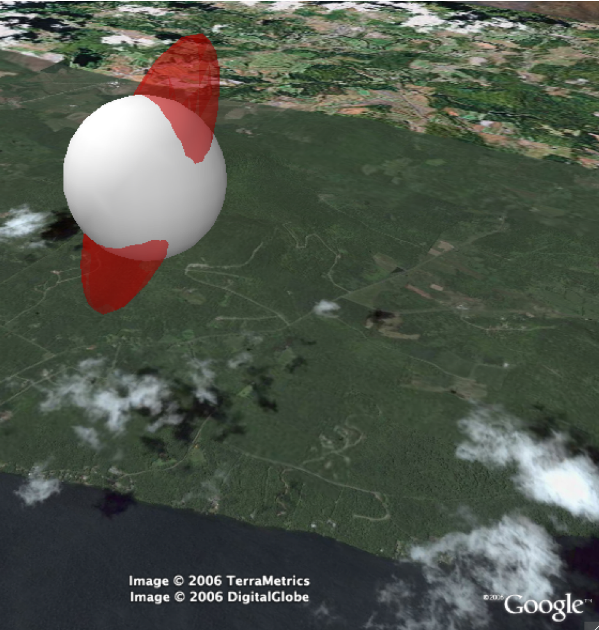
Alternative representation of CMT components using intersecting semi-opaque sphere and moment tensor eigen-ellipsoid. This sample does not represent a real event.
This line of intersection is a spherical ellipse and it defines a bi-cone of elliptical base – a non-planar nodal surface that separates directions of contractional and dilatational first motions just as the pair of nodal planes did in simple double-couple movements. The diagram may be thought of as a geophysical basketball. However, in special cases of spheroidal eigen-ellipsoids, the semi-major and semi-minor arcs of the spherical ellipse are equal, the cone has a circular base, and the diagram looks more like a geophysical pool ball (Figure 11b). A range of sample non-DC CMT solutions are available from the download file. For precise dimensions, it is most efficient to use the representation in Figure 11c which is created by superimposing a semi-opaque sphere and ellipsoid concentrically. Note in passing that a similar approach is ideal for representation of stress and finite strain data in 3 dimensions (De Paor & Pinan-Llamas 2006).