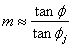FLAC (Fast Lagrangian Analysis of Continua, ICG, 1999) is a two-dimensional explicit finite difference program that is capable of solving a wide range of complex problems in continuum mechanics. It has been successfully applied to the study of a number of structural geology and rock mechanics problems such as strain localization [Hobbs et al., 1990; Ord 1991; Poliakov and Herrmann 1994], quartz c-axis fabric development in folds [Zhang et al., 1993, 1994], single-layer buckling [Zhang et al., 1996, 2000], and asymmetric boudinage [Passchier and Druguet, 2002]. The new version 4.0 allows interactive grid generation, boundary condition and material property definition as well as graphic presentation of the results. In particular, FLAC contains a powerful built-in programming language FISH (short for FLACish) that allows the user to write his/her own programs to extend FLAC’s functions including implementation of new constitutive models. FISH programs to derive kinematic histories of finite strain accumulation, vorticity, kinematic vorticity, and finite rotation have recently been developed in the Laboratory for Structural Geology and Tectonics at the University of Maryland. With these programs, it is possible to track the development history of any model-produced structures at required resolution.
The following observations of natural kink-bands suggest that the most likely rheology for their development is one of anisotropic plasticity. First, kink-bands are most common in low-grade rocks such as slates and phyllites. They may occur in higher-grade rocks, but wherever they occur, they are commonly identified as being late in the deformation history [e.g., Dewey 1965]. In mylonites, for instance, they occur as a late structure overprinting the C-foliation (Figure 1b). All this suggests that kink-bands have developed in low temperature environments in which rocks likely behave like plastic solids. Second, the very fact that kink-bands occur mostly as localized bands suggests that they are strain localization phenomena. It is an intrinsic material property for most plastic materials to develop strain localization [e.g., Hobbs et al., 1990; Ord 1991; Vardoulakis and Sulem 1995]. For viscous materials to develop strain localization, some mechanisms of material softening such as those associated with mylonitization must be invoked [e.g., Poirier, 1980; White et al., 1980; Hobbs et al., 1990]. There is no microstructural evidence suggesting that these mechanisms have operated during kink-band development. Third, kink-bands are observed in well-foliated rocks or anisotropic crystals, suggesting that rheological anisotropy might be important in their formation.
Figure 3. Rheology of a Mohr-Coulomb
In FLAC modeling, the rheology of a Mohr-Coulomb solid is a Mohr-Coulomb criterion with a tension cutoff (ICG 1999, p.2-19). It deforms elastically (yellow area) unless the failure criterion is met when the solid fails either by shear or tension. See text for more discussion.
We use the Mohr-Coulomb model to simulate plasticity, and the ubiquitous joint model to simulate anisotropy. A Mohr-Coulomb solid behaves elastically unless the Mohr-Coulomb yield criterion is satisfied (Figure 3). The material yields either by shear, for which the envelope criterion is:
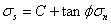
or by tension, for which the criterion is:
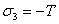
In equations 1 and 2, ss and sn are shear and normal stresses respectively, and s3 is the minimum principal stress (compressive stress is taken positive); C, f, and T are, respectively, the cohesion, friction angle, and the tensile strength of the material.
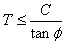
The ubiquitous joint model in FLAC is a Mohr-Coulomb plastic solid with an embedded penetrative weak plane (ubiquitous joint) of specific orientation. When a well-layered or foliated rock is viewed on the scale in which the layering or foliation is truly penetrative, the rheology of the rock can be simulated by the ubiquitous joint model. One can regard the rheology of the microlithon domain as the Mohr-Coulomb solid, and the foliation septum the ubiquitous joint. In a ubiquitous joint model, plastic yielding may occur either in the Mohr-Coulomb solid or along the weak plane, or both, depending on the stress state, the orientation of the weak plane and the material properties of the solid and the weak plane. The yield criteria of the weak plane (ubiquitous joint) are:
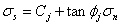
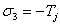
where the subscript j stands for ubiquitous joint, and:
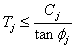
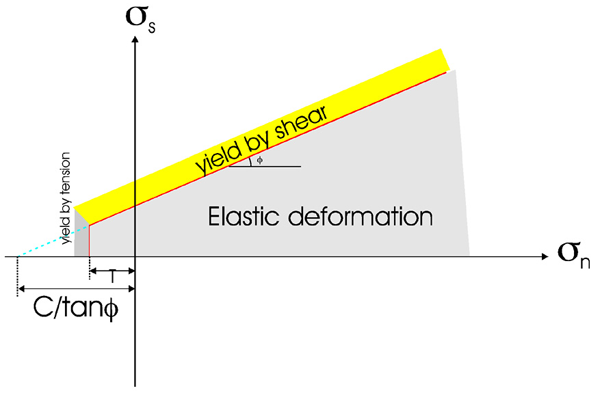
It can be readily seen that the ubiquitous joint model represents the simplest anisotropic plastic material, one with an axial symmetry. For such a material, similar to Ramsay and Lisle (2000, p. 778) and Treagus (2002), a parameter, m, can be defined to measure the degree of anisotropy. m is defined as the ratio of the shear strength of the Mohr-Coulomb solid to that of the weak plane:
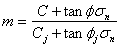
Clearly, m=1 represents the situation that the ubiquitous joint has the same strength as, and is mechanically indistinguishable from, the solid. The material is therefore isotropic. As m increases, the material becomes more anisotropic.
For rocks, the range of variation of Cj and C is from 10MPa to tens of MPa [e.g., Carmichael 1989]. The confining pressures under which kind-bands develop are well above 100MPa (>300MPa according to Anderson 1974). Therefore for conditions relevant to kink-band development, the stress conditions are always sn>>C or Cj. This can be used to simplify equation 5 to:
In the following, we present our modeling investigation on how the deformation mode of a ubiquitous joint model varies as m varies for given sets of material properties.