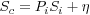Combination procedure
The strategy adopted in this work foresees the combination of the velocity solutions at the normal equation level. Each individual solution is inverted and the two normal matrices are compounded to form the global normal equation matrix, treating each site’s velocity and position as an independent observation. The combined normal matrix is then inverted again in order to estimate the unified velocity field and positions of the entire network and saved in the standard SINEX format.
Denoting with Si (i=1,2) the arrays of the site coordinate-velocity vectors of the i-th solution, the combined field (Sc) is estimated by solving in a least squares sense the following design equation where the design matrix, Pi (i=1,2) is simply the reordered matrix (reordering the i-th solution parameters into the combined parameters order) and η is the noise array.
Since usually the covariance matrix is known, apart from a solution-dependent variance factor, a scale factor is also estimated together with the combined solution. This assures that each solution’s contribution to the total χ2 is equally balanced, and individual solutions do not prevail in the combination because of differences in the uncertainties caused by unknown covariance matrix scaling factors. The estimated solution scaling factors ƒi fulfil the following condition between each i and j contributing solution:
where Ri = Si - Sc are the coordinate-velocity residuals. The Bernese solution incorporates 433 sites whereas the Gamit solution 378 and the final combined solution hold 481 site coordinates and velocities (481 x 6 parameters). The estimated covariance scale factors are 23.9 and 57.9, respectively, for the Bernese and Gamit solutions, while the reduced chi squared of the combination (variance factor) is 0.8.