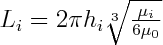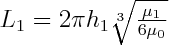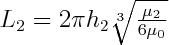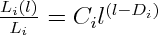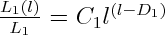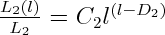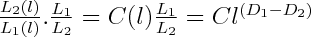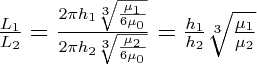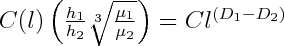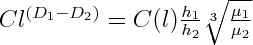Complex buckle folds with multiple orders can develop in isolated stiff layers in a less stiff matrix, a multilayered package where individual layers vary in composition and thickness, and also in homogeneous but anisotropic materials. Single-layer folds are much less variable than multilayered folds, so in this study, we restrict our investigation to complex folds developed by the buckling of a single isolated viscous layer in a less viscous matrix.
A very simple geometry is considered in this model, namely a single isolated layer within a homogeneous matrix deformed under conditions of pure shear, with the shortening direction parallel to the layer. This geometry is similar to that employed in many previous experiments using both elastic and viscous materials (e.g. Biot et al., 1964, Ramberg, 1964; Huddleston, 1973b), also, approximately symmetric single-layer folds are fairly common in nature (Sherwin & Chapple, 1968, Cobbold et al.1971). Most natural folds are highly variable and complicated due to the fact that they usually result from the rheological deformation on a geological time scale. For complex folds, the rheological deformation forms the major component while elastic deformation is negligible (Biot et al., 1964, Ramsay, 1967).
Many factors affect fold shape and development. There are too many unknowns to deduce rheological properties unambiguously from populations of natural folds. If a reasonable assumption about the form of the initial wavelength spectra is made, if strain in the competent layers can be measured independently, and if anisotropy is unimportant, estimates of rheological parameters can be made (Fletcher, 1974). Based on the experimental and theoretical rheology models, Biot (1964) and Ramberg (1964) proposed the theory of buckle folding, which predicts that, for a system consisting of an isolated stiff viscous layer in a less viscous matrix subject to layer-parallel pure shear, all harmonic components that are present in the initial irregularities of the layer interfaces will become amplified, with a maximum rate of growth occurring for the 'dominant wavelength' (Biot, 1964, Ramberg, 1964, Fletcher, 1974). For Newtonian materials, the dominant wavelength is a function of the thickness and the viscosity ratio, of which the expression can be given as:
Where Li is the dominant wavelength, µi is the viscosity of the layer i, µ0 is the viscosity of matrix, and hi is the thickness of layer i. The formula (2) also represents that, for Newtonian materials, the ratio of dominant wavelength to thickness is a function only of the ratio of viscosity of the stiff layer to the viscosity of the matrix.
The bigger the viscosity contrast between a stiff layer and the matrix is, the faster initial folds will grow. Two separated layers develop different folds during the layer parallel shortening in the same matrix, and seem to undergo different shortening. In fact, the layers and matrix undergo the same quantitive layer parallel shortening, but the contributions of layer parallel shortening and buckle folding are varied in different layers with other viscosities and thicknesses (Ramberg, 1964, Ramsay & Huber, 1987).
Here, we assume a model where the complexity of fractal folds is only affected by the viscosity and thickness in a single-layer buckling scenario. In comparison, two layers with different viscosities and thicknesses are each in a matrix with the same viscosity, given in the models (Figure 3).
In a matrix with viscosity of µ0, layer 1 with viscosity ofµ1 and thickness of h1, and layer 2 with viscosity of µ2 and thickness of h2, both develop fractal buckle folds 1 and 2 at the same strain, their dominant wavelength are L1 and L2, which are given by:
Based on the fractal theory (Mandelbrot, 1983, 1985, Falconer, 1990), the relationship between the fold arc Li(l) measured by the scale factor l and the dominant wavelength Li is given by:
Where L i, the dominant wavelength of fold i, is a reference length for normalization (Figure 1), Di is the fractal dimension of fold i, Ci is constant in equation (5).
For fold 1, the equation (6) is given by
For fold 2, the equation (7) is given by
The equation (8) is given from equation (6) and (7)
Where l is the scale factor, C = C2 / C1, C(l) = L2(l) / C1(l), L1 is the dominant wavelength of fold 1, L2 is the dominant wavelength of fold 2, L1 (l) is the arc length of fold 1 measured with respect to the scale factor l, L2 (l) is the arc length of fold 2 measured with respect to the scale factor l. D1 and D2 are the dimensions of fold 1 and fold 2 respectively.
Equation (9) is obtained from the equation (3) and (4):
thus, equation (10) is obtained from (8) and (9):
or
Figure 3. Four possible models of buckling in an incompetent matrix.
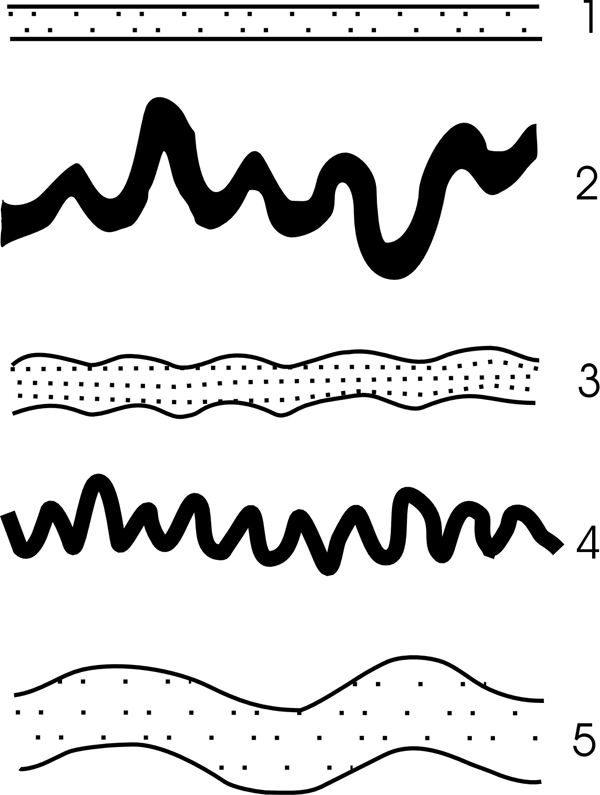
(a) Layer 1: long wave folding with more contribution from shortening. layer 2: easily develops snake folds. Layer 2 is more complex than layer 1 in where h1 > h2, µ1 >µ0 and µ2 >>µ0.
(b) Layer 1: easily develops complex folding with different orders, layer 2: small wave folding with more contribution from shortening. Layer 1 is more complex than layer where h1 > h2, µ1 >> µ0 and µ2 > µ0.
Figure 4. The results of buckling experiment
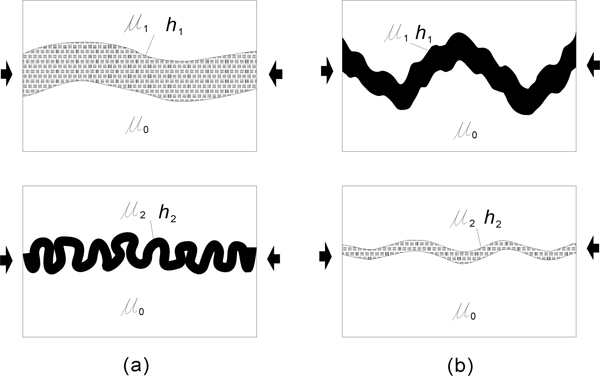
The results of buckling experiment in different rheological conditions where strain is constant (after Ramberg, 1964).
µ4 >µ2 >µ3 >µ5 >µ1 >µ0, h5>h3>h2>h1>h4
(µ1, µ2, µ3, µ4, µ5 and µ0 are the viscosities of layer 1, 2, 3, 4, 5 and matrix respectively, h1, h2, h3, h4 and h5 are thicknesses of layers 1, 2, 3, 4, and 5 respectively)
Based on the characteristics of fractal geometries, the dimension D is not related to the scale factor l, so C(l) is a variable constant related to l, but doesn't change the fractal dimension D. The difference (D1-D2) representing the complexity contrast between two fractal folds is controlled by the ratio of viscosities (µ1/µ2 ) and ratio of thicknesses (h1/h2 ) between two folds. The larger contrast of viscosities or thickness between two layers can yield greater difference (D1-D2) between two fractal folds. In nature, the viscosity contrast (µ1/µ2 ) is commonly much bigger than the ratio of two thicknesses (h1/h2 ). The viscosity contrast, therefore, plays a more important role in affecting the complexity of buckling folds of a single-layer than the thickness if only two factors (viscosity and thickness) are considered in the buckling. If the viscosity contrast is large, the fold will grow in amplitude at a rapid rate. The layers 2 and 4 are competent layers, developing more complex fractal folds than other incompetent layers (Figure 4). At a small or moderate viscosity contrast, there is a rapid increase in layer thickness by layer-parallel shortening and a slow growth of fold amplitude (Figure 5a). In the same strain condition, the competent layer experiences more buckle folding than layer parallel shortening, while the incompetent layer experiences more layer parallel shortening than buckle folding (Figure 5 a, b and c).
Figure 5. Viscosity and thickness constraints
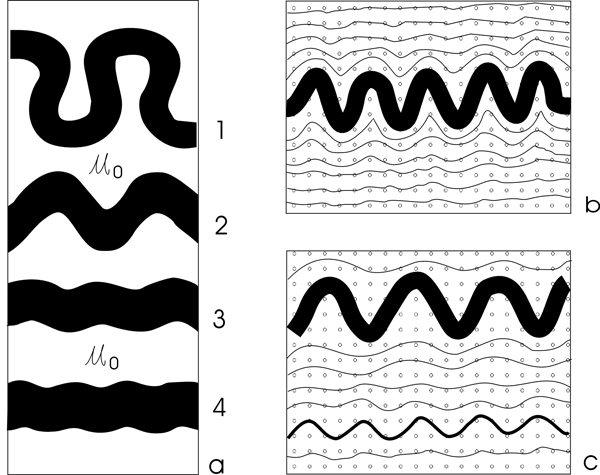
Viscosity and thickness constraints on the shape of fractal folds (after Ramsay & Huber, 1987).
(a) Folds with various viscosities (µ1>µ2>µ3>µ4>µ0, h1=h2=h3=h4), a higher viscosity contrast in a layer allows more buckle folding, µ1/µ0 > 50, 50 > µ2 / µ0 > µ3 / µ0 > 10, µ4 / µ0 < 10.
(b) Thicker competent layer (black) with greater amplitude and wavelength.
(c) The thicker of the two competent layers (black) has greater amplitude and wavelength.
The thickness of a layer also affects the complexity and harmony of folds. The thickness of a single-layer can control the shape of folds. Two single-layers with a higher thickness ratio are more disharmonic (Castro & Cashman, 1999). Assuming the same strain condition is applied, the thicker layer can develop a larger dominant wavelength and have more chance of developing complex folds with higher fractal dimensions than a thin layer, while the thin layer only develops small wavelengths (Figure 5 b and c). Layer 3 and 5 develop more complex folds than layer 1 (Figure 4). In general, a thicker layer with higher viscosity more easily develops more complex folds with larger fractal dimensions, filling more space than a thin layer with lower viscosity (Figure 3, comparing layer 1 with layer 2).
The equation (10) suggests that the coupling of at least two factors (viscosity and thickness) can produce different fold shapes and make complex folds. Otherwise, the fractal dimension difference between two folds can indicate the harmonic degree. Two folds are harmonic if the difference of two fractal dimensions (D1-D2) is zero. The larger the difference between the fractal dimensions of two folds is, the larger the disharmonic degree. This is supported by folds observed in the field (Castro & Cashman, 1999).
The formula (10) gives a theorical explanation to the experiment shown in Figure 4 and the formula is expanded to explain the complexity of the folds. In fact, the complexity of a fractal fold is affected by both the viscosity and thickness of a layer. This is a coupling effect, for example: a thick soft layer cannot form a complex fold and is mostly undergoes layer-parallel shortened. The complex folds with large fractal dimensions result from the coupling of greater thickness and higher viscosity of a single-layer. In the buckle folding experiment, a thin competent layer can easily develop folds with a small wavelength, and a thick layer can develop folding with a big dominant wavelength. Therefore the thick competent layer can develop complex folds with varying characteristic wavelengths in different orders of folding. The viscosity and the thickness contrast between layer and matrix are very important in affecting the complexity of fractal folds. In nature, a thick layer with a low viscosity contrast usually develops layer-parallel shortening, the thin layer with high viscosity usually develops ptygmatic folds, and commonly the thick, competent layer develops complex folds including many orders. In conclusion, the coupling of two rock properties (viscosity and thickness) can produce complex folds and affect the fractal dimension of complex folds.