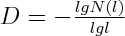Most natural folds are not as simple as those generated by physical and numerical models, producing folds that are smooth and linear. Natural folds are usually complex, nonlinear and composed of many orders of folding of different magnitudes. The anticlinorium and synclinorium commonly developed in any orogenic belt are self-similar, called a fractal pattern. In the field, the so-called 'S','Z','M' and 'W' parasitic folds are observable from different parts of some outcrop-scale folds. This scaling property of the folds ranges from tens of kilometers of compound folds in orogenic belts, to folds in outcrop and sample scale, and even to micron scale, indicating that the natural folds are of the fractal geometry (Wu, 1993). The anticlinorium and synclinorium are formed by superimposing smaller scale folds. The order of a complex folds is distinguished from the neutral surfaces or the enveloping surfaces of the fold (Turner & Weiss, 1963, Ramsay, 1967, Ramsay & Huber, 1987). Natural folds commonly have three orders (Figure 1).
Figure 1. Fold with three orders identified
The model showing a fold with three orders identified by the neutral surfaces of the fold
Self-similarity of structure is an important characteristic of fractal geometries, in which any portion of the system is a scaled-down version of the whole ( Mandelbrot, 1983 ). A feature of a fractal geometry is that the relative numbers of large and small elements remain the same at all scales between the upper and lower fractal dimension, which is simply derived from the power-law exponent on a plot of log ruler (l) vs. log cumulative number(N) (Formula 1) (Mandelbrot, 1983).
Most natural folds are complex, variable, and develop many fold orders with self-similarity in fractal patterns. They can therefore be described quantitively by fractal geometry (Wu, 1993, Hou, 1998). Complex folds can be simulated by fractal interpolation and classified into different populations by their complexity relative to the fractal dimension D (Hou, 1998).
Where D is the fractal dimension of the fold, with a value between 1.0 and 2.0 in two dimensional space.
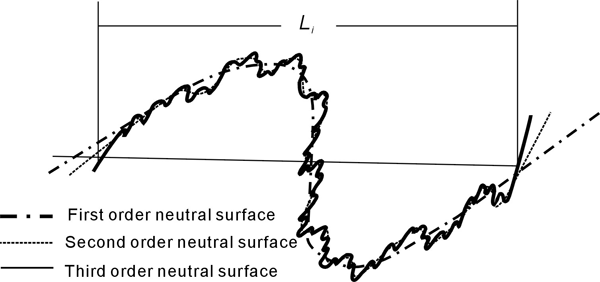
A fractal fold profile is, defined by Mandelbrot (1983), as a curve with a fractal dimension (D) greater than its topological dimension. A topological dimension is an integer such that a discrete point has a topological dimension of zero, a curve of 1, and so on. The fractal dimension of a fold profile describes how much of the two-dimensional space it fills. The fold with bigger amplitude and more orders of folding means it fill more of the space, and so its fractal dimension is larger. If a fold profile consists of a simple line without any curve, its fractal dimension D = 1. If a fold profile is so complicated that it almost fills the entire space, its fractal dimension D will be close to 2. Thus, most fractal fold profiles have a fractal dimension 1 < D < 2 (Wu, 1993; Hou, 1998). Thus, the complexity of a fold can be described by the fractal dimension (D), with more complex folds usually having a larger value of D (e.g. Figure 2). Obviously, the fold with D of 1.48 (correlation coefficient=0.996) is more complicated than the fold with D of 1.38 (correlation coefficient=0.996).
There are two basic types of fractals: one is self-similar, the other is self-affine (Mandelbrot, 1985), and both are statistically defined (Power & Tullis, 1991). The self-similar fractal fold has a constant amplitude-to-wavelength ratio, while an important aspect of a self-affine fractal is that the self similarity is not universal and changes with scale (Wu, 1993, 1995). Most natural fractal folds are self-affine fractals.
Figure 2. Two fractal folds with different complexities
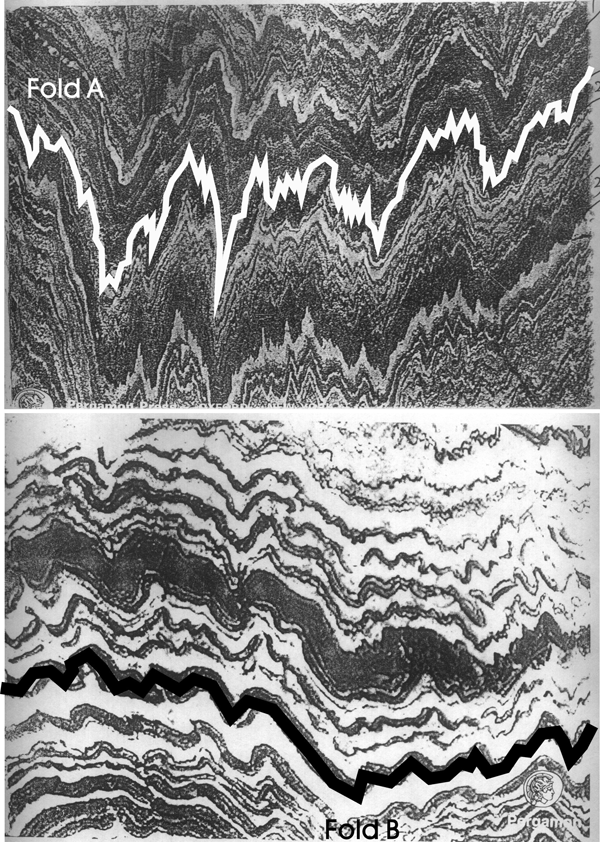
Two fractal folds with different complexities (different fractal dimensions)
A: Folds in banded hornblende gneiss in the core of the Maggjia Nappe from Fusio, Ticino, Switzerland;
B: Folds of calc-silicate layers in marble,Neoproterozoic deposits in the Khan River Gorge, Central Namibia