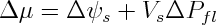Dissolution precipitation creep is an important deformation mechanism in the Earth's crust. It plays a major role in the compaction of sedimentary basins and in the building of mountain chains [Weyl 1959; Rutter 1976; Spiers et al. 1990; Schwartz and Stöckert 1996]. The mechanism involves dissolution of material at sites of relatively high stresses, transport through a fluid phase and precipitation of material at sites of relatively low stresses. Most research has focused on the dissolution at confined contacts between grains [Paterson 1973; Lehner 1995; Schutjens and Spiers 1999; Dysthe et al. 2002 a, b]. However, recent experiments and theoretical considerations indicate that free surface dissolution may also be important [den Brok and Morel 2001; den Brok et al. 2002]. In the present paper we focus on free surface dissolution of stressed crystals and illustrate how concentrations of elastic energy can lead to instabilities and localization of dissolution.
At the contact of a crystal to the fluid, dissolution and precipitation are driven by differences in chemical potential along the interface. On free interfaces shear-forces in the fluid can be neglected so that changes in the chemical potential can be defined as [Gibbs 1906; Kamb 1961; Paterson 1973]
where μ is the chemical potential, ψs the Helmholtz free energy of the solid, Vs the molecular volume of the solid and Pfl the fluid pressure and the deltas represent changes in these values relative to a reference state. The Helmholtz free energy contains contributions due to surface, elastic and plastic energy. In the present study we focus on surface patterns on stressed elastic crystals in contact with fluid so that we neglect effects of plasticity. Patterns on the surface will then depend on competition between local elastic and surface energies as long as the fluid pressure does not change.
Recent experiments on brittle elastic salt crystals show the development of a roughening instability on the free solid/liquid interface [den Brok and Morel 2001; den Brok et al. 2002]. In the experiment a crystal of an elastic salt is stressed vertically while its surface is in contact with under-saturated brine. The crystal surface develops a roughness that consists of grooves oriented with their long axis perpendicular to the main compressive stress direction. The roughness on the crystal surface has a distinct spacing or wavelength that depends on the stress state of the crystal and its surface energy [Srolovitz 1989]. The grooves on the crystal surface develop because the chemical potential (Equation 1) is higher when the crystal is stressed so that it dissolves. Stress concentrations at troughs of the roughness increase dissolution, which again has a positive feedback effect on the stress. This effect is known as the Asaro-Tiller-Grinfeld instability [ATG, Asaro and Tiller 1972; Grinfeld 1986]. Linear stability analysis of the onset of the ATG-instability [Srolovitz 1989] predicts that dissolution structures will develop with a roughness that lies within a band of stable wavelengths and thus have a characteristic spacing as observed in the experiments [den Brok and Morel 2001].
The progressive evolution of the ATG-instability and the evolution of patterns beyond this instability have been studied using numerical simulations [Yang and Srolovitz 1993; Ghoussoub and Leroy 2001; Kassner et al. 2001]. In the simulations an initial roughness develops into cusp instabilities and then evolves towards crack-like structures or anti-cracks. In the current paper we will present a new approach to model the ATG-instability and its evolution towards anti-cracks [Koehn et al. 2003] and grooves [Koehn et al. 2004]. First we introduce the numerical method. Then we show the development of the initial ATG-instability and compare the patterns with linear stability analysis and existing numerical simulations. In addition we illustrate the propagation of anti-cracks and finally present combinations of anti-crack propagation and mode I cracking (Mode I Fractures are tensile fractures that grow perpendicular to a tensile stress component, Anti-cracks are lens shaped structures that grow by dissolution or reaction at their tips perpendicular to a compressive stress).