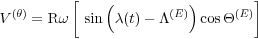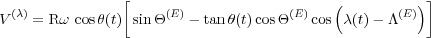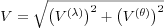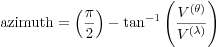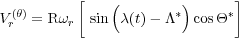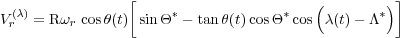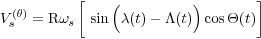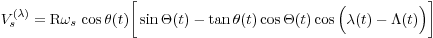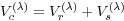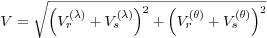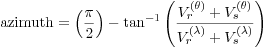Theory and method
Though the application of Euler.s theorem for plate kinematics (Bullard et al. 1965) is always valid, independently of the choice of relative or absolute reference frame, plate motion is principally using relative kinematic analysis, (Cox and Hart 1986, Fowler 1990, Turcotte and Schubert 2001). Present-day motion of a single plate can be described as an instantaneous rigid body rotation on a spherical surface about an Euler pole (Figure 1a). In the simplest case, as time goes on, the plate has a fixed pole of rotation, and any point in the plate maintains the same distance from the pole while the plate moves. Then each point on the plate simply rotates around the pole, travelling on a circular trajectory.
Here, we propose an analytical method that describes this simple motion of one plate point, giving, as the result, the velocities of the transversal and longitudinal displacement depending only by the point coordinates. Because the plate is rigid, its kinematics can be studied starting from geometrical considerations, obtaining motion equations without any dynamical treatment.
Considering the Earth as a sphere, spherical trigonometry (Ayres 1954, Butler 1992, Fowler 1990, Turcotte and Schubert 2001) allows derivation of two equations that describe respectively the velocity of the transversal and of the longitudinal displacement of a single plate point (see appendix A) as follows:
where (Θ(E), Λ(E)) are respectively the latitude and the longitude of the Euler pole that are time-independent, (θ(t),λ(t)) are the coordinates of the generic plate point that is time-dependent, and where ω is the angular velocity. Because the motion is smooth and steady, V(θ), V(λ) and ω are constant. Then, the expressions to obtain the magnitude and the azimuth of the velocity of a geographical plate point are the following:
Equation (4) ensures that zero is aligned with the true north to correspond to the geological convention of measuring direction of strike (Henderson 2001).
Equations (1-4) do not differ from the results of Stein and Wysession (Stein and Wysession 2003) and Zhong (Zhong 2001).
In this paper, we consider that a generic lithospheric plate is moving on a spherical surface in an absolute reference frame, making two contemporaneous rotations, one about an external 1st rotation pole, and another about an internal pole (sub-rotation pole), inside the plate that moves with the plate itself (Figure 1b). During the continuum of time, the plate still moves about the 1st rotation pole, but it contemporaneously rotates around the sub-rotation pole, and one reference point of the plate changes its distance from the main pole, shown at two different times t1 and t2, increasing and decreasing the distance from the main pole (Figure 1b) and making a particular trajectory like an epicycloid (Figure 2). Only one point does not change its distance with the main pole, and this is the sub-rotation pole. This rotates about the 1st pole and makes a circular trajectory (Figure 2). If the motion is considered without such a decomposition, at every instant there is a different instantaneous pole of rotation, the (composed rotation pole) (Figure 3). A succession of such poles would be necessary to describe the real motion, whereas the two stage decomposition allows the motion to be described simply.
Figure 3. Composed rotation pole
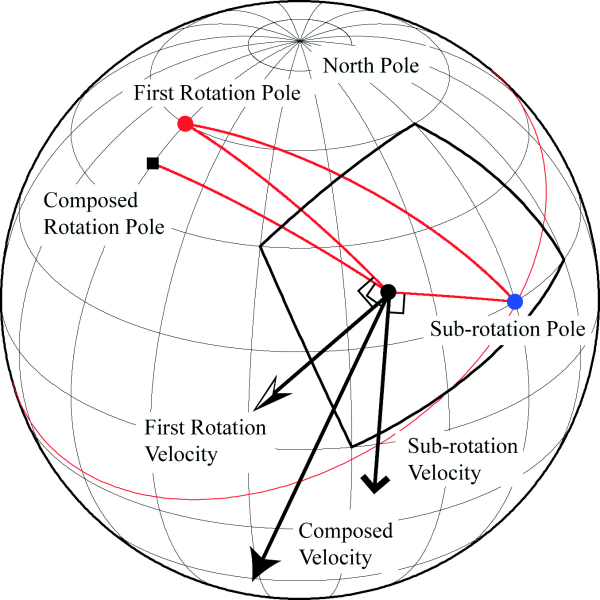
When plate motion is composed by a first rotation and a contemporaneously subrotation, one reference point is characterized by two linear velocities, one relative to the first rotation pole and the other relative to the sub-rotation pole. The sum of these two velocities is the composed velocity related to a third pole of rotation, (composed rotation pole).
Butler (1992) describes the motion of a single plate as a rotation with respect to an internal rotation axis and with respect to an external Euler pole, but he considers two different and separated cases. In the two separated situations only one angular velocity and one Euler pole are required. Using the two rotation model, with one the internal and one external axis, we need two angular velocities, one (ωr ) related to the 1st rotation and the other (ωs) related to the sub-rotation. Then equations (1) have to be applied twice, the 1st time for the 1st rotation and the second time for the sub-rotation. In this case, using equations (2) at one generic plate point two linear velocities are applied that represent the action of the angular velocities (Figure 3). The resulting velocity is a vector that is instantaneously related to the composed rotation pole that during the continuum of time, changes its position every instant.
Then considering the 1st rotation, we have the following:
where (Θ*, Λ*) are respectively the latitude and the longitude of the 1st rotation pole, and these are time-independent. (θ(t), λ(t)) are the coordinates of the generic plate point, and these are time-dependent. ωr is the 1st rotation angular velocity.
Considering also the contemporaneous sub-rotation, equation (1-2) can be written as follows
where (Θ(t), Λ(t)) are respectively the latitude and the longitude of the sub-rotation pole (time-dependent), (θ(t), λ(t)) are the coordinates of the generic plate point (also time-dependent) and ωr is the sub-rotation angular velocity.
Adding the two contemporaneous rotations, e.g. 1st rotation and sub-rotation, we obtain the expression of the composed movements as follows:
where Vc(θ) and Vc(λ) are respectively the velocity of the transversal and longitudinal composed displacement of a single plate point. In this case, the expressions to obtain the magnitude and the azimuth of the velocity of a geographical plate point are the following:
and the velocity of the generic plate point obtained with equation (6) is generally related with a third pole of rotation (composed rotation pole), that is not significant in showing the pattern of the overall movement (Figure 3).
For the purpose of separating the two-rotation motion, we need to know the motion parameters as the 1st rotation pole coordinates (Τ*, Λ*) and the 1st rotation angular velocity ωr and then, the sub-rotation pole coordinates (Θ(t), Λ(t)) and the sub-rotation angular velocity ωs.
If we try to ascertain the two-rotation motion of a plate in an absolute reference frames, e.g. the hotspot frame (Chase 1978, Gripp and Gordon 1990, 2002) or the GPS frame (Heuin et al. 2004) the secondary rotation needs to be separated from the primary motion.
To 2nd the motion parameters, we have to examine tectonic aspects that suggest a two-rotation motion, as indicated in the example of Iberia. Potentially the present day plate motion or the actual plate motion from space geodesy for a single plate can be interpreted as a 1st rotation and a contemporaneous sub-rotation.
Using the GPS velocties solution (Heuin et al. 2004) and the actual plate motion model APKIM2002, (Drewes and Meisel 2003) we tried to apply equations (6) to the North American plate, hypothesizing that the instantaneous North American plate motion can be viewed as the result of the sum of two different rotations, one an external 1st rotation and the other a contemporaneous sub-rotation.