Introduction
Plate motion analysis has been computed in a number of different ways, from magnetic anomalies [Vine 1966], seismology, hotspots [DeMets et al. 1990], [Gripp and Gordon 1990] and space geodesy data [Sella et al. 2002], [Drewes and Meisel 2003]. Plate movements can be described both in absolute reference frames, e.g. the hotspot reference frame [Morgan 1972], [Wilson 1973], or relative reference frames, e.g., one plate relative to another (Chase 1972, Minster and Jordan 1978, DeMets et al. 1990, Gordon 1995). For sake of simplicity, the motion of a plate can be described, in an analytic way, as a rigid body rotation around an Euler pole over the Earth.s surface.
Considering the motion of plates in an absolute reference frame, parts of a plate, while it is rotating about the same Euler pole as the remainder, can make a further contemporaneous rotation with respect to another pole. For example, along with the rifting between Eurasia and North America in the Late Cretaceous and Early Cenozoic, Iberia has rotated counter-clockwise, producing the extension in the Bay of Biscay and most of the shortening in the Pyrenees (Van der Voo 1993). From an absolute motion point of view the 1st-order rotation pole of the Iberia plate was the same of the Eurasia plate, but there was another sub-pole that was contemporaneously involved in the extension of the Bay of Biscay.
Figure 1a. Plate moving on a sphere about an Euler pole.
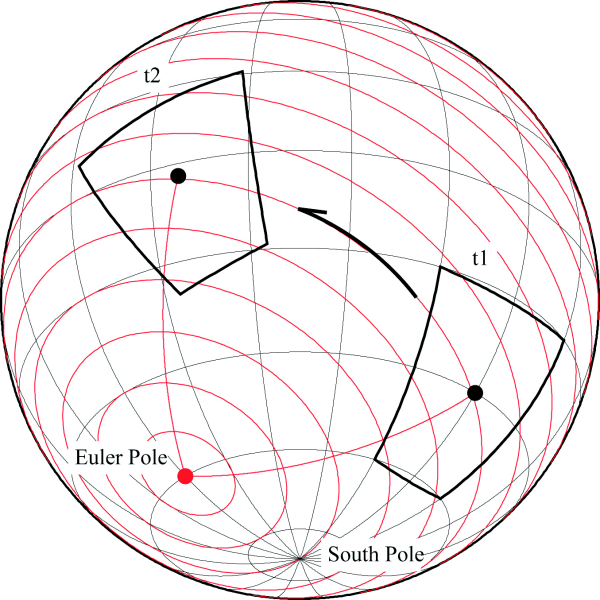
For the simplest case (a) a plate moves on a sphere constantly rotating about an Euler pole. A point in the plate maintains the same distance from the pole, here shown at two different times, t1 and t2.
Figure 1b. Plate moving on a sphere about an Euler pole.
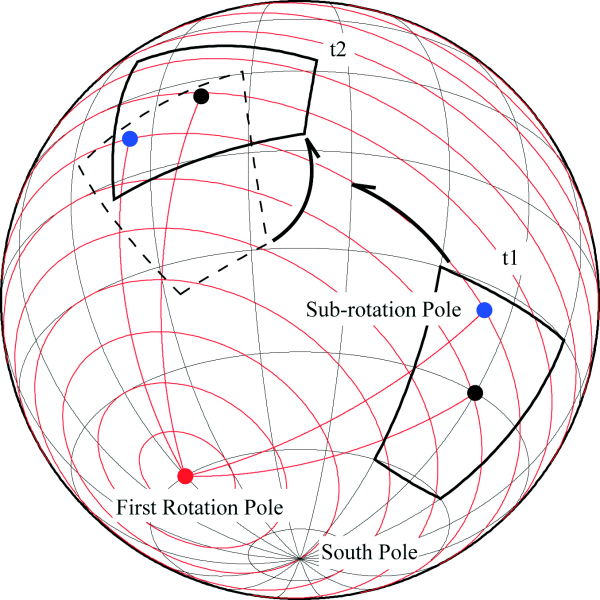
When plate motion is described by two simultaneous motions (b), the plate is rotating about a 1st rotation pole while contemporaneously rotating about a sub-rotation pole. Any reference point in the plate changes its distance from the main pole, shown here for two different times, t1 and t2, e.g., increasing or decreasing its distance from the main pole. Only one point does not change its distance from the main pole, and this is the sub-rotation pole that defines the axis of the second rotation.
It is clear that relative kinematic analysis, made for example by the NUVEL-1 relative plate motion model [DeMets et al. 1990] does not allow the hypothesis of sub-rotation, to be verified, because the motion of rigid plates is described, and only one rotation is necessary for plate kinematics. When the relative motion of one plate respect to a second plate is computed, the relative rotation of sub-plates is taken into account either by averaging, or it is ignored. Plate motion models relative to hot spots, such as HS2-NUVEL1 or HS3-NUVEL1A [Gripp and Gordon 1990, 2002] or with the no-net-rotation condition, as NNR-NUVEL1 (Argus and Gordon 1991) also do not recognize the sub-rotation of some plates, because again these are an adaptation of the relative plate motion model NUVEL-1 [DeMets et al. 1990].
For the case of Iberia, in fact, its rotation can be studied relative to Eurasia considered as fixed, and only one angular velocity and one rotation pole is sufficient to describe the motion. But the Eurasia plate was rifted from North America and the Iberia plate has also felt the effect of this motion, and it has followed the Eurasia trajectory. Incremental motion can always be described by a single rotation pole and a rotation. Angular velocity can similarly be described by a rotation pole and an angular velocity. But if we seek an expression that does not change with every instant, two angular velocities and two rotation poles are required to describe the Iberia plate motion.
The previous example focuses attention on plate motion over geological time, where to determine the rotation of a plate and sub-rotation of its elements, paleomagnetism and plate reconstructions have to be involved. We can also consider present-day plate motions in this context, seeking a decomposition of present day motions into elements that involve rotation poles fixed with respect to material coordinates. The NNR reference frame, NNR-NUVEL1 (Argus and Gordon 1991) is based on geological and geophysical data acquired on plate boundaries. Actual plate motion models, REVEL2000 (Sella et al. 2002) or APKIM2002 (Drewes and Meisel 2003) are based on the space geodesy techniques. In these cases also the instantaneous rotation of a plate can be viewed as composed of a primary rotation and a sub-rotation (if required). This decomposition can be performed if the instantaneous pole of rotation will change its material location with time. Under such circumstances points on plates do not move on circular trajectories, but they describe curves that resemble parts of epicycloids projected on the Earth's surface (Figure 2). In reality a plate the plate points chosen would describe only segments of these epicycloids, because insufficiently large rotations would accumulate on the second pole.
Figure 2. Plate motion described by two rotation poles.
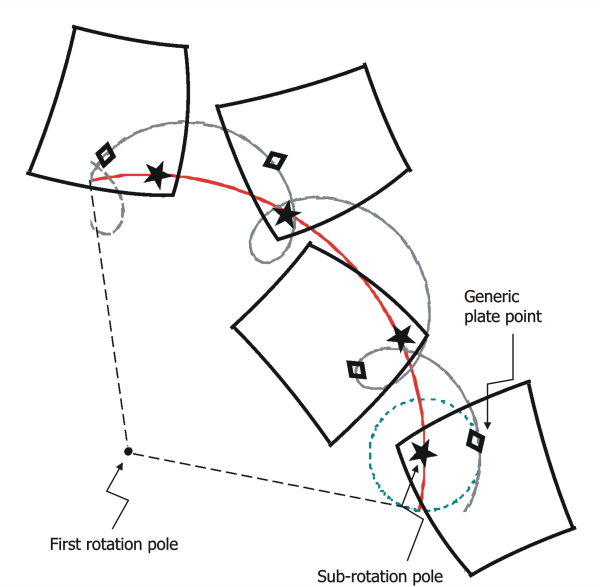
Plate motion when two rotation poles and two angular velocities are required. The plate rotates about the 1st rotation pole while it contemporaneously rotates around the sub-rotation pole. A random point in the plate changes its distance from the main pole at (here) shown at four different times and positions, making a trajectory like an epicycloid (gray line). Only one point does not change its distance with the main pole, and that point becomes the sub-rotation pole. This will make a circular trajectory (red line) around the main pole. For sake of simplicity the two-rotation motion is shown here for a plane, but the decmposition is also valid on a spherical surface. This plate is moving CCW about the 1st rotation pole, at the same time it is sub-rotating CCW about the sub-rotation pole. In reality, the motion of a plate would allow definition of only part of this epicycloidal trajectory.
The importance of detecting sub-rotation in absolute reference frames concerns the dynamical implications, and hypotheses about global plate tectonics. Regardless of the forces that move plates, in general sub-rotation of a sub-plate requires the action of a torque, as in the example of Iberia.
In this paper we describe an analytical method that decomposes the motion of a single plate in an absolute reference frame into a combination of two contemporaneous rotations: a primary rotation around a main pole of rotation (1st rotation pole) and a secondary rotation (sub-rotation) around a second pole. To illustrate the method we used present-day plate motions from the NASA database (Heuin et al. 2004) and the actual plate motion model APKIM2002 (Drewes and Meisel 2003) applied to the North American plate. In the ITRF2000 reference frame the instantaneous motion of the North American Plate (NA) can be interpreted as a combination of two contemporaneous rotation: we can view its motion as the combination of a westward drift, but with a further internal CCW rotation.