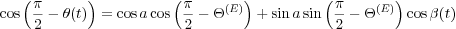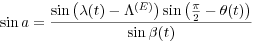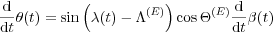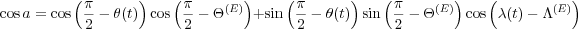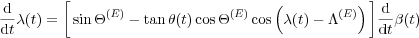Appendix A. The equations of motion
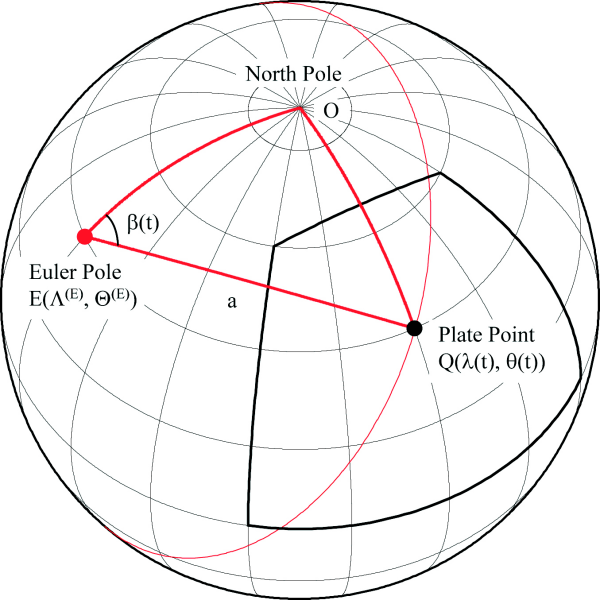
During plate motions, choosing the North Pole (O) as the origin of the coordinate system, in the spherical triangle OEQ (Figure 8), the length of the arc a = EQ, is an invariant relative to the time. In a sphere of a unit radius, from spherical trigonometry rules (Ayres 1954), we have:
Figure 8. Simple plate motion
For the simple plate motion, in the spherical triangle OEQ, Q is the generic plate point, E is the Euler pole, and the length a = EQ is an invariant during plate motion.
and differentiating the (A1) relative to the time, using the (A2) and simplifying, we obtain:
Now, considering the Earth as a sphere with a radius R=6371 km, being V(θ) = R.(δ/δt)θ(t) and ωr = (δ/δt) β(t), we obtain the velocity of the transversal displacement as equation (1).
To calculate, instead, the velocity of the longitudinal displacement, we consider the following:
and differentiating the (A4) relative to time, using (A3) and simplifying, we obtain:
Then, considering the Earth as a sphere with a radius R=6371 km, being V(λ) = R.cos θ(t)(δ/δt)θ(t) and ω= (δ/δt)β(t), we obtain equation (2).
When we separately consider the two components of the composed motions, e.g., the 1st rotation and the sub-rotation, there are two spherical triangles, (OP*Q and OPQ) (Figure 9), and for simple motion, the lengths b*=P*Q and b = PQ are invariant. For this reason we can calculate the velocities of transversal and longitudinal displacement, respectively, for the 1st rotation and the sub-rotation (equations 5-6), with the same procedure as for the simple case, but writing ωr = (δ/δt)α*(t) and ωs = (δ/δt)α(t). When we add the two components in equation (5), the length b* =P*Q is not invariant with time and one reference plate of the plate changes its distance from the 1st rotation pole during motion (Figure 1).
Figure 9. First rotation and the sub-rotation
When the motion is composed by a first rotation and the sub-rotation, there are two spherical triangles, OP*Q and OPQ, and the lengths b* = P*Q and b = PQ are separately invariant. Applying equation (5) the length b* = P*Q is not invariant during the motion. The only point that moves along the parallel of the first rotation pole is the sub-rotation pole.