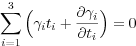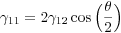Textural Equilibrium
Textural equilibrium is reached when a material has minimized the energies bound up in interfaces and within individual grains (Figure 1a). This state can only be attained once the material is defect-free and in chemical and mechanical equilibrium. The free energy of an interface in an isotropic system (i.e. the energy of the interface is constant regardless of its orientation relative to any crystal lattice) is typically of the order 1 Jm-2 (Sutton and Baluffi, 1996), and is a function of its curvature (Harker and Parker, 1945). The chemical activity of a system with curved interfaces is higher than that in a system with planar interfaces (Bulau et al., 1979). Because of this, all interfaces must have the same mean radius of curvature. This can only be attained in isotropic systems if grain-size is uniform.
For anisotropic substances, certain orientations of the surface have a lower energy than others and so it is possible to reach a minimum energy state with a mixture of planar and curved surfaces (Herring, 1951a; Waff and Faul, 1992). This is particularly important for geological materials such as amphiboles (Figure 1b) and sheet silicates, although grain boundaries in even relatively isotropic quartz have significant planar regions (Kruhl, 2001; Kruhl and Peternell, 2002; Leibl et al., 2007).
A further constraint is that the energies of the interfaces at three- and four-grain junctions must be in mechanical equilibrium, satisfying:
where γ1, γ2, γ3 are the three interfacial energies, ti is the vector in the plane of the ith surface, normal to the line of intersection of the surfaces and pointing away from this line, and ∂γi/∂ti is a vector perpendicular to ti and to the line of intersection (Herring, 1951b). The tangential component of this equation acts to minimize the surface area, while the normal component rotates the interface towards an orientation with a lower interfacial area.
For an isotropic polycrystalline material, in which the interfacial energy is constant regardless of the orientation of the interface, the normal term vanishes: three-grain junctions therefore meet at 120˚, while the four three-grain junctions where four grains meet are 109˚28’ apart. For poly-phase junctions the angle between two inter-phase boundaries is known as the dihedral angle (Smith, 1948; 1964), and for two-phase junctions in isotropic systems the simplified form of this equation becomes:
where γ11 is the energy of the boundary between two grains of phase 1, γ12 is the energy of the inter-phase boundary, and θ is the dihedral angle (Figure 1c).
Figure 1. Texturally equilibrated microstructures

(a) epidote-hornblende quartzite (sample 87974 from the Cambridge Harker Collection) showing microstructural evidence for a close approach to textural equiibrium. (b) detail of the rock shown in (a), showing an amphibole grain surrounded by quartz. The shape of the amphibole is dominated by {110} faces (parallel to the cleavage which is picked out by white lines). These faces are particularly low energy and so form part of the equilibrated microstructure. (c) The dihedral angle, θ, is formed by balancing of the interfacial energies at three-grain junctions. (d) Texturally equilibrated amphibolite (Aboyne, Deeside, sample 102032 from the Cambridge Harker Collection). The white lines show the tangents to the curved grain boundaries. The dihedral angles at the three-grain junctions should be measured between these tangents.
However, all geological materials have some form of anisotropy (e.g. Kretz, 1966; Schafer and Foley, 2002) and so there is no single value of the equilibrium dihedral angle (Herring, 1951b; Laporte and Watson, 1995; Laporte and Provost, 2000; Kruhl, 2001): the angle varies according to the relative orientation of the grains at the junction with a greater spread of possible angles for the more anisotropic minerals (e.g. Vernon, 1968; Laporte and Provost, 2000). The least anisotropic minerals (i.e. those with a tighter spread of equilibrium angles) include quartz, calcite and feldspars, while the most anisotropic include micas and amphiboles (Laporte and Watson, 1995).
In texturally equilibrated melt-bearing rocks, the melt-solid-solid dihedral angle has significant consequences for rock physical properties via its underlying control on melt topology (Takei, 2000; Yoshino et al., 2005; Hier-Majumder et al., 2006; Price et al., 2006; Parsons et al., 2008; Pervukhina and Kuwahara 2008). In isotropic systems in which the liquid-solid-solid dihedral angle falls below a critical value of 60˚ the liquid phase remains interconnected along a series of channels on three-grain junctions down to vanishingly low porosities. However the facetted pore walls present in equilibrated anisotropic materials mean that this connectivity is broken when the porosity falls below a few vol. % (Minarik and Watson, 1995; Laporte and Watson, 1995; Yoshino et al., 2002; Cheadle et al., 2004; Yoshino et al., 2006; Price et al., 2006). In open systems the porosity is also a function of the dihedral angle: melt is either infiltrated or expelled as the system attempts to attain the value of porosity at which the interfacial energy budget is minimized. This minimum energy porosity reaches a maximum value of ~ 20 vol.% for angles of 60˚, declining to zero for angles above 60˚ (Park and Yoon, 1985; Laporte and Watson, 1995).
The last stage of textural equilibration (termed "textural coarsening" by Higgins (2010)) involves grain growth. This has the effect of reducing the connectivity of any melt phase with a dihedral angle greater than 60˚ due to what is called “pinging off” of melt-filled channels on three-grain junctions (Bagdassarov et al., 2009). Because the end point of energy minimization is when the material comprises infinitely large defect-free grains, true textural equilibrium is only ever approached and never reached.