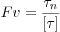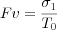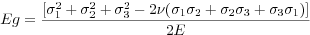Bio-Factor Method for prediction of structural fractures
The Bio-Factor Method employed here was originally developed by Ding, et al. (1998), in which the two factors refer to Fracture Value derived from stress-related Fracture Laws and Energy Value obtained from strain energy. The combination of these two factors is realized through the simulation formula of Bio-Factor, which requires a large number of trials to obtain the coefficients in the formula by the fitness between the calculated fracture density and the statistic fracture density.
The most common prediction method for structural fractures is based on stress, rock strength and rock fracture criteria, such as Mohr-Coulomb criterion. In this study Fracture value (Fv) is redefined (Wang, et al., 1980):
σn is the shear stress on the shear-crack plane, while [σ] is shear strength. Fv<1 at a certain point indicates unfractured, while Fv=1 fractured. Furthermore, if Fv>>1 at a certain point, it indicates the rock has fractured long before and Fv<<1 indicates that the rock is far from fracturing.Thus the results are more quantitative rather than just predicting whether the rock has fractured or not.
For tensile fracture, we employ the formula:
Where s1 is the maximum of the tension force, and T0 is tensile strength.
A close perusal of the Table 4 indicates that the co-efficient between Fv and Fd is very weak (e.g. Fv at O5, O11, and O26) and so a better method is needed for the predictions, taking into account of the strain energy also.
The elastic strain energy in each unit is used to define Energy Value (Eg), which can be calculated based on the results of stress field through the following formula:
Where σ1, σ2 and σ3 are the three principal stresses, E and ν are Young's Modulus and Poisson's Ratio respectively which can be obtained from rock mechanical properties (Table 3). The Strain Energy at a particular point can be calculated from the three principle stresses at that point. Once more, it turned out to be that the coefficient between Eg and statistic Fd is also weak (Table 4, Column 5).
As there is no fit between Fv and Fd, as well as between Eg and Fd, another method X2 has to be employed for solving the problem.
Table 4. Data from Statistics and Predictions of Es3 for Each Well in the Study Area
| Well | X-axis | Y-axis | Fracture Value Fv | Energy Value Eg | Statistic Fracture Density Fd | Predicted Fracture Density Fd | Absolute Error (1/cm) | Relative Error (%) |
|---|---|---|---|---|---|---|---|---|
| O1 | 27.9 | 16.2 | 1 | 10.69 | No Core | 0.3883 | Null | Null |
| O2 | 16.6 | 15 | 0.9 | 5.03 | No Core | 0.1551 | Null | Null |
| O3 | 16 | 17.7 | 0.99 | 9.73 | No Core | 0.3481 | Null | Null |
| O5 | 41.7 | 19.7 | 1.06 | 19.12 | 0.79 | 0.7548 | -0.0352 | 4.5 |
| O6 | 32.5 | 18.3 | 1.01 | 6.09 | No Core | 0.2194 | Null | Null |
| O7 | 26.8 | 18.6 | 1.02 | 0.47 | No Core | 0.0074 | Null | Null |
| O8 | 24.2 | 16.4 | 0.99 | 8.19 | 0.2968 | 0.2914 | -0.0054 | 1.8 |
| O10 | 34.2 | 20.5 | 1.25 | 1 | No Core | 0.0358 | Null | Null |
| O11 | 29.5 | 18.3 | 1.02 | 10.64 | 0.4245 | 0.396 | -0.0285 | 6.7 |
| O12 | 39.4 | 18 | 1.03 | 0.98 | 0.0235 | 0.0272 | 0.0037 | 15.8 |
| O13 | 35.7 | 17.8 | 0.98 | 15.74 | No Core | 0.5623 | Null | Null |
| O14 | 22.3 | 15.9 | 1 | 5.13 | 0.1358 | 0.1809 | 0.0451 | 33.2 |
| O15 | 28.5 | 17.3 | 1 | 2.88 | 0.0874 | 0.097 | 0.0096 | 11 |
| O19 | 17.6 | 16.1 | 0.64 | 5.61 | 0.1076 | 0.1096 | 0.002 | 1.9 |
| O24 | 33 | 17.3 | 0.97 | 6.71 | No Core | 0.2309 | Null | Null |
| O26 | 24.2 | 17.3 | 1.11 | 14.28 | 0.5888 | 0.5933 | 0.0045 | 0.8 |
| O27 | 24.2 | 14.1 | 1.02 | 2.88 | 0.0968 | 0.0995 | 0.0027 | 2.7 |
| O28 | 23.1 | 17.8 | 1.26 | 3.12 | 0.1164 | 0.1406 | 0.0242 | 20.8 |
| O29 | 21.2 | 15.4 | 0.9 | 6.68 | 0.2084 | 0.209 | 0.0006 | 0.3 |
| O30 | 37.2 | 17.3 | 1.08 | 1.78 | 0.0708 | 0.0617 | -0.0091 | 12.8 |
| L10 | 26.8 | 15.9 | 1.02 | 12.14 | No Core | 0.4533 | Null | Null |
| L12 | 15.4 | 16.2 | 0.97 | 5.5 | No Core | 0.1874 | Null | Null |
| X3 | 39.5 | 12.3 | 0.93 | 11.61 | 0.4065 | 0.3859 | -0.0206 | 5.1 |
| J1 | 39.9 | 6.1 | 0.77 | 0.35 | No Core | 0.0014 | Null | Null |
| J4 | 49 | 6.8 | 0.81 | 0.95 | No Core | 0.0187 | Null | Null |
| J12 | 35.7 | 6.7 | 0.79 | 0.39 | No Core | 0.0026 | Null | Null |
Unit Note: Eg: J×104/m3; Fd: 1/cm.
Bio-factor Method
Bio-Factor Method in the form of polynome yielded by a large number of tests is as follows:
From Fv, Eg, and Fd (Table 4, Column 6) , the obtained coefficients are as follows:
The Bio-Factor Simulation Formula for Olituoz area employed here to predict the fracture density (Table 4, Column 7) is flexible by changing the coefficients in the formulae. The predicted results around the boundaries (the boundaries of the predicted area shown in Fig.4) are not reliable due to the boundary effect of calculation, especially the high values near the left boundary in Fig.4.
The calculated results are checked by comparing to the statistic data, and the errors are given in Table 4. The result is highly accurate and credible: of the total 13 wells, the errors of 10 wells are less than 15%, 8 are less than 7%. However, there are some unexpected results. The reasons and solutions for the high error data around well 028 and well 014 are to be studied further and need more future research.
Figure 4. Quantitative prediction result map derived from Bio-Factor Method
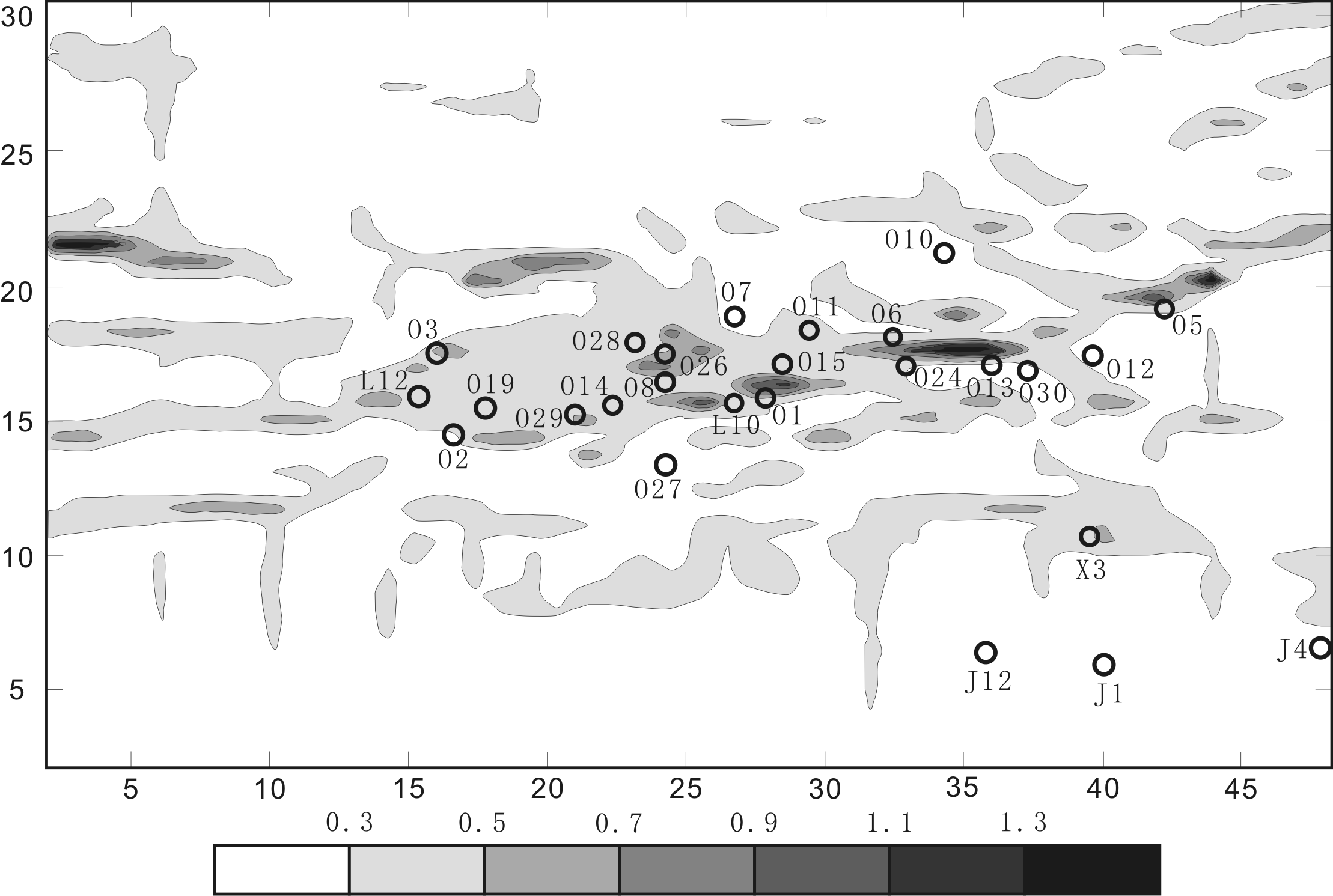
The prediction area are shown in Fig.3b as the ABCD. The contour lines stands for the Predicted Fracture Density.
Based on quantitative prediction, the areas with high density of structural fractures are demarcated (the region surrounded by O26, O8, L10, O1 and O15, areas around O5, northwest of O28, and the region surrounded by O11, O6, O13 and O24) (Fig. 4). These areas with Fd>0.9 are with high probabilities of forming fracture reservoir, which are the potential areas of drilling for oil.
In comparison to the faults (Fig. 3b), the main areas with high density of structural fractures are consistent with the NE-NNE trending faults in Olituoz area. Another evident feature is that the distribution of high density is arranged in left-en-echelon which resulted from dextral shearing.
These features compelled us to pay attention to the pre-existing faults in the region. According to Tuckwell et al. (2003) and Zeng et al.(2007), the pre-existing long fractures would dominate the local stress field and the stress are concentrated near the former faults, giving rise to intensive fractures. At the same time, the strain energy influenced by the pre-existing faults or fractures, triggers an additional strain energy (Li & Liu, 2008). Overall, the fracture development and distribution is controlled or strongly affected by the former fault system in the region.