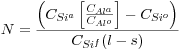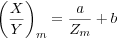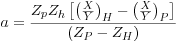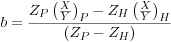5. Discussion
5.1. Origin of ‘beard’ structures
The quartz-biotite ‘beards’ described previously appear to be unusual in mylonites, where smaller ‘tails’ or ‘wings’ attached to well separated porphyroclasts in an abundant, fine-grained matrix are more common. In the Cerro de Costilla rocks, the abundance of large plagioclase clasts may have controlled the development of ‘beards’ by protecting lower-strain zones between the clasts, attracting components in solution, and promoting nucleation of quartz and mica on the plagioclase. We interpret the beards as indicating solution of biotite and quartz components in high-mean stress or high-strain sites and transport of components in solution to low-mean stress sites, where they nucleate as minerals on the plagioclase clasts, the mineral alignment defining the stretching direction.
Beards are common on clasts in low-grade deformed rocks, such as slates (e.g., McClay, 1977; Powell, 1982; Cox and Etheridge, 1982, 1983; Gray and Wright, 1984; Waldron and Sandiford, 1988; Gray and Willman, 1991; Vernon, 2004). For example, quartz-white mica ‘beards’ between quartz clasts in deformed quartz-rich sandstone have been illustrated by Dunlap and Teyssier (1998, fig. 86B). They have also been described in high-grade mylonitic rocks. For example, Lafrance and Vernon (1993, 1998) described hornblende beards on former pyroxene grains in mylonitic metagabbro, and Wintsch and Yi (2002) described beard structures in granodioritic orthogneiss. A variation on this theme is provided by oriented symplectites of orthopyroxene and plagioclase on garnet in mafic mylonites described by Brodie (1995, 1998). In both these gabbroic examples, growth of the beards was associated with breakdown and partial replacement of the clasts on which the beards were growing.
Creep by dissolution and precipitation may occur at high temperatures during deformation in the presence of water, as noted by Lafrance and Vernon (1993, 1999) for gabbro deformed at high-temperature amphibolite facies conditions, and by Wintsch and Yi (2002) for granodioritic orthogneiss deformed at 500-600°C. Lafrance and Vernon (1993, 1999) inferred that plagioclase flowed by dislocation creep and recrystallized, but that pyroxene and hornblende mainly fractured and developed fringes of aligned grains (beard structures) between boudins. Wintsch and Yi (2002) inferred that, though biotite and quartz deformed by dislocation creep, most of the deformation was accomplished by deformation-enhanced dissolution of minerals at grain boundaries perpendicular to the shortening direction — indicated by truncated zoning patterns in plagioclase, orthoclase, epidote and titanite — and precipitation in the form of beards on the ends of grains that faced the extension direction. Both of these examples show that solution-precipitation creep can accompany and even dominate over dislocation creep at high temperatures in the presence of water.
5.2. Metasomatic alteration
The modal and chemical changes across the shear zone suggest that fluid-rock interaction and mass transfer occurred synchronously with deformation (e.g., Lonka et al, 1998; Barnes et al., 2004; O’Hara, 2007). In this section, the geochemical data described above are used to estimate the amount of fluid that may have been involved and explore the possibility of fluid-enhanced chemical mixing between the marginal Cerro de Costilla and the host rocks.
5.2.1. Fluid-rock ratios
The volume of externally-derived fluid that interacted with the shear zone rock is estimated through the calculation of fluid-rock ratios. The calculations are based on an inferred increase in bulk SiO2 during metasomatic alteration (Table 1) relative to the designated immobile species (Al2O3, TiO2, and Zr). Fluid-rock ratios (N) were calculated from average SiO2, Al2O3, TiO2, and Zr whole-rock concentrations (C) using the equation:
(after O’Hara & Blackburn, 1989), where a = altered samples (B and C), o = protolith samples (D-J), CSif = SiO2 solubility in the fluid, and s = SiO2 saturation in the fluid,. N was calculated for silica saturation values of 0%, 25%, 50%, 75%, and 95%, and a SiO2 solubility of 3g/kg was assumed, in accordance with the approximate temperature of deformation (Fournier & Potter, 1982). Ratios calculated using the Al2O3, TiO2 and Zr reference frames are all nearly identical, namely 0.25-6.0 for SiO2 saturations between 0%-95% (Table 5). The presence of recrystallized quartz-rich pods and strain shadows in sheared marginal rocks suggests that SiO2 saturation may have approached 100% (at least locally), and thus actual fluid-rock ratios may be closer to the high end of the above range (approximately 6.0).
Figure . Table 5.
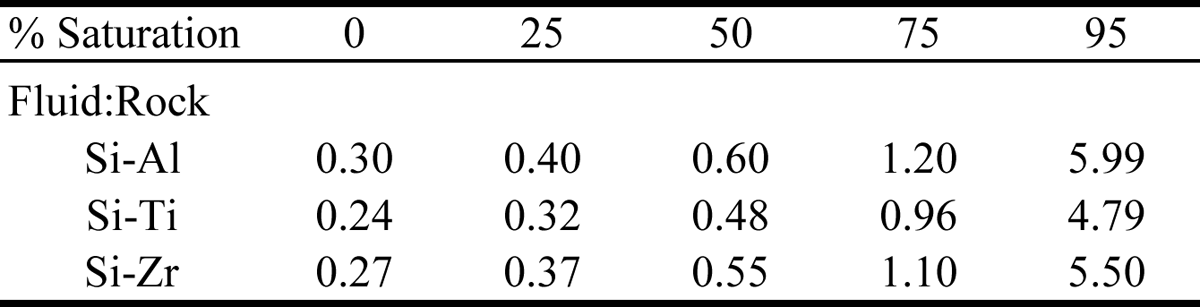
Fluid-rock ratios calculated from bulk geochemical changes (after O’Hara and Blackburn, 1989).
5.2.2. Two-component mixing model
To determine whether the bulk compositional changes observed in samples A-C could have resulted from chemical exchange with the host granitic gneisses (i.e., local mass transfer), two-component mixing models were constructed from bulk chemical data using groups of three elements X, Y, and Z in the form of binary plots of X/Y vs Z (after Yang et al., 1998). The hyperbolic mixing curves between end-member compositions have the general form:
where m denotes the mixed composition of interest, and a and b are obtained from the tonalitic protolith (P) and host rock (H) end-member compositions, such that:
Major and trace element concentrations of the average interior tonalite samples (D-J; protolith) and from published chemical data on granitic orthogneisses (host rock) from the Pine Valley Suite of the Peninsular Ranges batholith (Todd et al., 2003) were used in the calculations (Table 1).
Mixing curves calculated for the “mobile” major elements generally show close agreement with the observed concentrations in the marginal samples. The observed concentrations of SiO2, K2O, CaO, Fe2O3, and MgO in marginal samples B and C plot close to the curves predicted for a two-component mixture (Fig. 38). Na2O concentrations in the marginal samples are much lower than in both the unaltered tonalite and host gneisses, and thus a bulk leaching of Na2O from the sheared margin is suggested. Overall, most major element concentrations in the marginal Cerro de Costilla are consistent with fluid-assisted mixing of chemical components from the tonalite protolith with those of the adjacent host rocks during deformation, although alternative explanations cannot be ruled out.
Figure 38. Two component mixing model for undeformed Cerro de Costilla tonalite and host granitic orthogneiss.
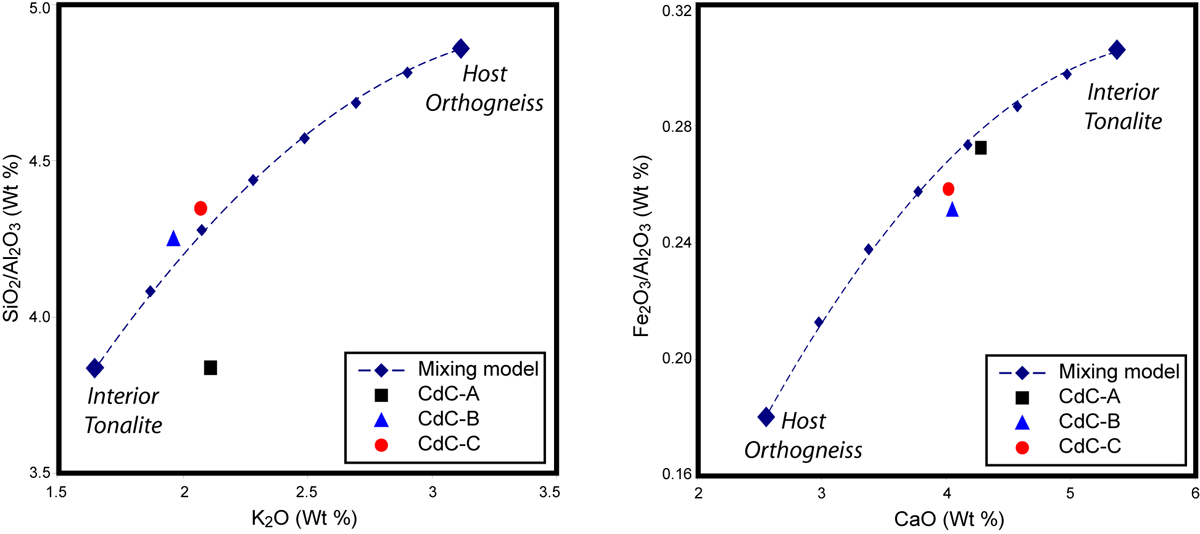
Two component mixing model for undeformed Cerro de Costilla tonalite and host granitic orthogneiss. Concentrations of mobile elements SiO2, K2O, CaO, and Fe2O3 within the sheared margin plot close to the theoretical mixing model curves calculated for the undeformed tonalite and host orthogneiss end members.
5.3. Coupling of mechanical and chemical processes in strain localization
Microstructural observations, combined with chemical data indicate that the coupling of mechanical and chemical processes played an important role in the development of mylonitic fabric evolution and modal changes in the shear zone. The occurrence of small new grains of biotite and fragmental plagioclase along grain boundaries and fracture surfaces indicates that fracturing and dilatancy of the plagioclase framework enabled localized fluid access and grain growth along the newly exposed surfaces (e.g. Fitz Gerald & Stünitz, 1993, Collettini & Holdsworth, 2004; Marsh et al., in press). With increasing strain, the main physical and chemical processes involved in the fabric evolution were: (1) fragmentation and cleavage slip of biotite, (2) recrystallization and dislocation creep of quartz, (3) fragmentation and granular flow of plagioclase, hornblende, titanite and rare epidote, (4) replacement of hornblende by biotite, (5) solution/re-precipitation of biotite and quartz, (6) replacement of rare K-feldspar by myrmekitic intergrowths, followed by recrystallization and dislocation creep of these aggregates, and (7) replacement of biotite by symplectic titanite-plagioclase intergrowths, followed by fragmentation and/or recrystallization and dislocation creep and/or granular flow of these aggregates.
As continuous biotite-rich foliae developed, and fine-grained quartz and biotite precipitated behind plagioclase grains to form ‘beards’, the increased interconnectivity of the fine-grained matrix enhanced the effective permeability of the rocks, allowing faster diffusion/advection rates (e.g. Carlson & Gordon, 2004) through an intergranular fluid phase. In the most highly strained rocks (samples A-C), strain appears to have been increasingly accommodated by dissolution-precipitation creep, as evidenced by synkinematic precipitation of biotite and quartz, although dislocation creep remained active in quartz. The development of a sharp microstructural and mineralogical front between samples C and D suggests strong coupling among fluid, reaction and strain in the most highly deformed rocks (samples A-C). We infer that the development of a continuous foliation and reduced grain size with proximity to the pluton margin enhanced effective permeability, and thus enabled the efficient fluid mobility and element exchange required for the reactions to proceed. In this narrow (1-m) zone, reaction rates may have increased sufficiently to keep up with bulk strain-rates (e.g. Baxter & DePaolo, 2004; O’Hara, 2007).
A conceptual illustration of fluid-chemical-mechanical coupling is shown in Fig. 39. In this framework, deformation is described through the velocity gradient tensor, effective viscosity being the controlling physical parameter. Intergranular mass transport is described by diffusion and fluid advection. Reactions are described through a rate equation. Various interactions, or couplings, are illustrated among the three principal processes. Coupling of deformation and reaction is manifest by hardening or softening of rock as a function of mineralogical change, and is thus the simplest representation of interaction between the velocity field and rheological evolution. This coupling also facilitates strain-sensitive reaction in which deformation increases the number of paths for reaction progress. Coupling of deformation and diffusion can arise through diffusion and/or advection terms. Note that the diffusion, advection, reaction equation treats the full velocity field around a point, so that deformation is also expressed through an advection term. Stretching and folding of material due to deformation changes diffusion lengths and fluid pathways, which can serve to reduce or eliminate the time-dependent decay of chemical potential gradients (e.g., Ottino, 1989). Deformation also changes the microstructure, typically leading to grainsize reduction and more efficient grain-boundary transport paths. Coupling between diffusion/fluid advection and reaction rate can be expressed, for example, through the evolution of porosity and the spatial dependence of thermodynamic affinity.
Figure 39. Coupling of deformation, reaction and diffusion/advection in the transformation of tonalite to mylonite.
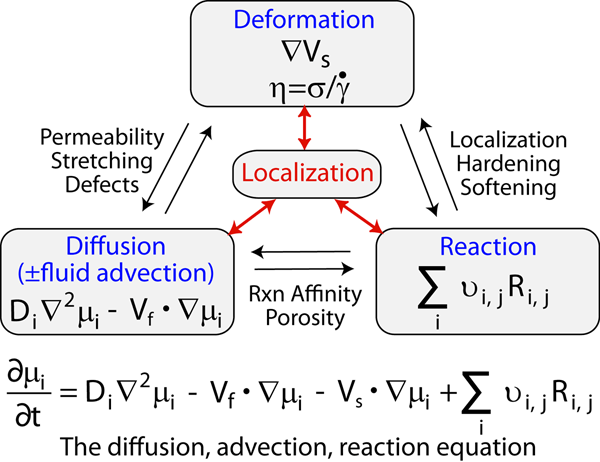
Transformation of tonalite to mylonite framed as a three-way coupling among deformation, diffusion/advection, and reaction. ∇ = the gradient operator, V = velocity, η = viscosity, σ = shear stress, γ̇ = shear strain rate, D = diffusion constant, μ = chemical potential, υ = stoichiometric coefficient, R = rate of production or depletion, subscript i = species, subscript j = reaction, subscript f = fluid and subscript s = solid. Important limiting assumptions in the diffusion, advection, reaction equation include: (1) Di is spatially constant, and (2) transport processes and chemical reactions do not affect the mechanics. Modifications to the equation can reflect changes in the mechanics, as defined by changes in rheology, with time.
5.4. Rheological effects
In the Cerro de Costilla, coupled microstructural and chemical processes led to strain-dependent weakening and strain localization mainly by: (1) the progressive breakdown by fracturing, fragmentation and reaction of the load-bearing plagioclase framework; (2) the progressive development of continuous biotite-rich foliae; (3) flow of quartz into lenticular foliae once the restricting plagioclase framework had sufficiently broken down; (4) elimination of strong hornblende accompanied by modal increase of weaker biotite; (5) dissolution, transport and re-deposition of biotite and quartz components in lower shear-strain sites between zones of continuous biotite-rich foliae; (6) overall grain-size reduction through fragmentation, recrystallization and neocrystallization of the main minerals; and (7) minor contributions from fine-grained aggregates of other minerals.
The end result of these processes is the development of a fully interconnected weak matrix studded with isolated plagioclase porphyroclasts. This type has been referred to as an interconnected weak phase (IWP; Handy, 1990) or weak phase supported (WPS; Ji et al., 2001; Takeda and Griera, 2006) microstructure, and has been shown to approach an iso-stress state (Reuss model) and a strength minimum (Ji, 2004; Takeda and Griera, 2006). The strength of the rock should therefore approach the strength of the dominant interconnected matrix mineral, which in this case is biotite. Micas are known to be among the weakest minerals in shear along their (001) planes at upper greenschist to lower amphibolite facies conditions, which are consistent with mylonite development in the Cerro de Costilla rocks (e.g., Kronenberg et al., 1990; Tullis and Wenk, 1994; Niemeijer and Spiers, 2005). Recent numerical (Johnson et al., 2004) and laboratory (Holyoke and Tullis, 2006; Mariani et al., 2006) experiments provide some guidance on how much weakening could be expected during the development of the most highly strained rocks studied here.
Johnson et al. (2004) combined detailed microstructural analysis of a preserved strain gradient within the sheared margin of the San Jose pluton in Baja California, México with grain-scale numerical modelling to explore the rheological effects of progressive coalescence of weak minerals. Johnson et al. (2004) showed that deformation was initiated by localized fracturing of the plagioclase framework near the tips of isolated biotite grains – as described here and by Marsh et al. (in press). Progressive development of continuous foliae occurred almost entirely by mechanical processes, leading to a mylonitic foliation in the most highly strained rocks at the pluton margin. Johnson et al. (2004) conducted numerical experiments to evaluate the initiation of these shear zones. With a starting geometry based on the least deformed portions of the pluton and general shear boundary conditions, localized zones of high differential stress and shear-strain rate developed in the “plagioclase” matrix adjacent to the tips of weak “biotite” grains. The localized zones of high differential stress reached values up to 2 times the confining pressure, leading to failure of the matrix and initiation of microshear zones. With continued deformation, elongate high strain-rate zones linking weak “biotite” grains developed across “plagioclase” bridges, these zones accommodating shear strain rates up to 2.5 orders of magnitude greater than in the adjacent matrix.
Similar results were obtained by Holyoke and Tullis (2006a, b), who conducted triaxial shear experiments on fine-grained quartzofeldspathic gneiss containing approximately 13 vol. % biotite. At the early stages of deformation, slip on biotite (001) planes caused microfaulting in quartz grains separating biotite grains. With continued strain, biotite interconnection occurred by localized semi-brittle flow of the quartz. At higher shear strains (γ≈3), through-going biotite-bearing microshear zones developed, coincident with a maximum stress drop of approximately 40%. At this advanced stage, shear strain rates within the microshear zones were approximately two orders of magnitude greater than in the adjacent rock, as found in the modelling of Johnson et al. (2004).
Mariani et al. (2006) conducted triaxial shear experiments designed to investigate the shear strength of continuous muscovite foliae in faults and shear zones. They used wet pressed polycrystalline muscovite layers with {001} planes at 45° to the loading axis, and pore water pressures of approximately 100 MPa to inhibit dehydration reactions in experimental runs spanning temperatures of 400 to 700°C. At relatively low strain rates and high temperatures, they observed marked strength drops, and the mechanical results suggest linear viscous creep. Mariani et al. (2006) concluded that mica-rich rocks may flow at shear stresses as low as 1-10 MPa at strain rates of 10-13 s-1 and temperatures consistent with upper greenschist to lower amphibolite facies metamorphism.
Given the results of these three studies, it is possible that the strength of the Cerro de Costilla rocks dropped from the frictional strength of plagioclase at approximately 10 km depth under hydrostatic fluid pressure conditions in a subvertical extensional fault to perhaps 10 MPa or lower. Such a strength drop would be close to an order of magnitude, but the lower bound is constrained by viscous basal creep in mica. Given that strain in the most deformed shear-zone samples was accommodated also (maybe largely) by dissolution/precipitation processes, we speculate that coupling of deformation, diffusion, fluid advection and reaction in the wet core of the mylonite zone may have allowed strain to accumulate at even lower shear stresses.