40Ar/39Ar geochronological analysis
White micas occur as ‘books’ of grains aligned in micro-scale shear zones (Figure 6) within a groundmass that is mica-poor. White micas within the groundmass are very small (<20 µm), are interstitial to other larger grains and have not been analysed due to their fine-grained nature. In contrast, the white micas in the mica-rich zones are characteristically large (<1000 µm) but also some small grains occur (~100 µm). It is the grains from these zones that have been used in this argon geochronology study. Grains selected for analysis included grains that were between 150 µm and 350 µm. Smaller grains, seen as the darker grains in the backscatter image, were not selected so as to eliminate potential recoil during analysis. However these darker regions still occur in the analysis at the margins and ends of larger grains.
A carefully designed furnace step-heating experiment on the irradiated white mica was carried out Particular care was taken monitoring background levels and maintaining low levels of contamination both at the start and during analysis. The furnace itself was checked for contamination and degassed four times to 1450 °C for 30 minutes. A total of 33 mg of single grains are wrapped in tin foil and dropped into the furnace where the foil was melted and then left at 420 °C overnight for contaminants (e.g., H2O, CO2) to be pumped away prior to analysis. The first step began at 450 °C, 26 steps were run in total with the heating schedule set so as to maintain the percentage of gas release as even as possible over the experiment.
The apparent age spectrum (Figure 11) that resulted from the step-heating experiment is as near perfect replica of what might be expected as the result of diffusional loss of argon from a fractal diffusion network (McDougall and Harrison 1999). The repetitiveness of degassing the furnace and extra time taken with these ‘cleaning’ procedures has decreased the contamination in the results. Likewise the extensive heating schedule starting at 450 °C has reduced the mixing of different gas populations and allowed the degassing of different gas populations to be released independently and be recorded.
The apparent age spectrum has five steps (between 910-990 °C of the schedule) that record an age of 55.7 ±0.3 Ma (MSWD 11.9) (with an overall 39Ar release of 38.5%). An older age of 61.1 ±0.3 Ma occurs towards the end of the experiment (Table 1 in Appendix A.). The York Plot (Figure 11c) shows a cluster of points, that correspond to the 55.7 Ma steps on the age spectrum, and mixing points up to the 61.1 Ma step. This implies that a range between 55.7 Ma and 61.1 Ma is possible.
The initial steps released very low 39Ar and give the youngest gas populations. The first step (with 0.05% 39Ar release) is at 22.7 ±10.3 Ma (a high error), however the second step gives an age of 16.5 ±4.7 Ma from with 0.10% 39Ar release. The steps from 1 to 6 have variable amounts of atmospheric Ar, followed by a moderate diffusion loss from step 7 (740 °C) to the plateau at 55.7 ±0.3 Ma.
The age spectrum from the white mica shows characteristics of diffusive Ar loss, with a 39Ar release pattern comparable to K-feldspar diffusion experiments and associated fractal feathering where information on different domains is preserved (Forster and Lister 2010). As a consequence simulation and modelling has been possible on white mica, a process normally restricted to K-feldspars (Lovera et al. 1997), which has allowed us to test if the results had geological meaning.
The Arrhenius plots presented in 40Ar/39Ar geochronology reflect the pattern of gas release from the different microstructural reservoirs or diffusion domains within the analysed grains. These data can be analysed to extract the activation energy and frequency factor normalised against the square of the diffusion domain radius. Theory for this purpose is set out for modelling K-feldspars using multiple diffusion-domain theory (or MDD models, Lovera et al. 1997). When Arrhenius data are analysed assuming a MDD model, the Fundamental Asymmetry Principle (FAP) must be obeyed (Forster and Lister 2010). The Fundamental Asymmetry Principle (or FAP) is implicit in any MDD model. "The FAP applies to any line fitted to data from a sequence of step-heating experiments in which the temperature applied from step to step may be the same, or higher, but may not decrease. Lovera et al. (1997) set out the basis of the MDD method, and shows how a straight line can be fitted to a set of Arrhenius data points, under specific circumstances. The fitted line will faithfully replicate the essential Arrhenius parameters only as long as the data points are derived from a set of partially degassed diffusion domains. Mathematically, to be consistent with a MDD model, any line fitted to any sequence of Arrhenius points must divide the population by rank order. Points from data obtained earlier in the sequence of step-heating experiments must lie on the fitted line, or to the right of it. Points from data obtained later in the sequence must lie on the fitted line, or to the left of it. A feathering effect is observed when the smaller diffusion domains are very much smaller than the larger domains” (Forster and Lister 2010, page 23). If the FAP is violated a derived MDD model will produce erroneous results, for numerically the method utilised will lead to consistently underestimated values for the activation energy (E) and for the normalised frequency factor (D0/r2).
Figure 11. 40Ar/39Ar apparent age spectrum
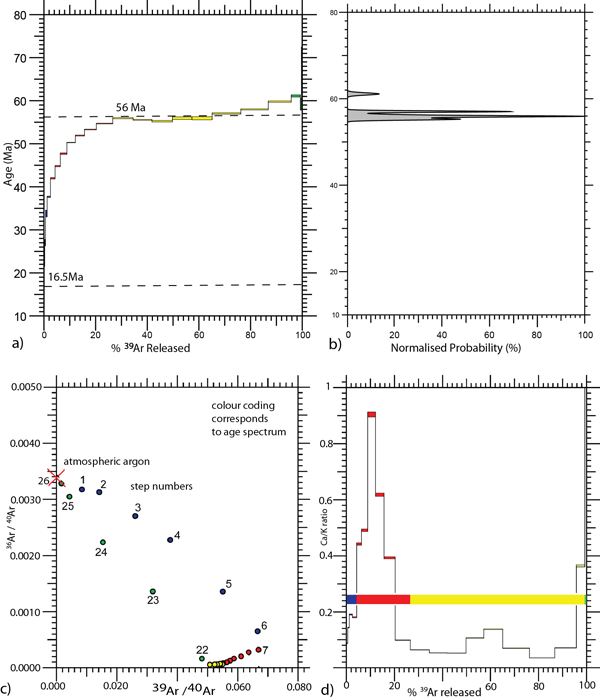
a) 40Ar/39Ar apparent age spectrum, the first step and plateau at the mid-temperatures of the experiment are marked with a dashed line. The green and final four steps represent the break down of the grains. Spectrum is colour coded so as to be able to correlate with the other graphs; b) Gaussian plot highlighting main gas release %; c) York plot with the points labelled with their step number and colour coded to match other graphs; d) Ca/K plot also colour coded to match other graphs.
Figure 12. Arrhenius plot for white mica experiment
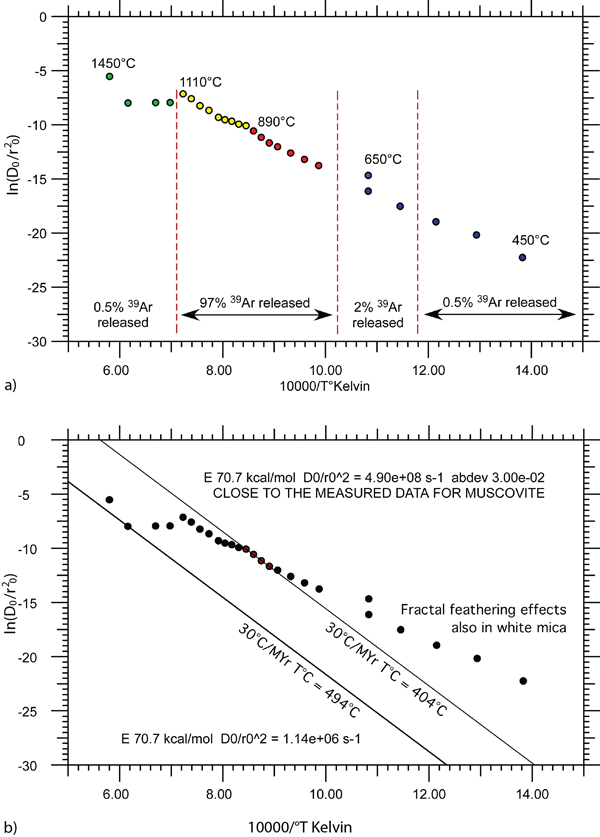
a) % gas release illustrated for the different stages of the apparent age spectra. The cusp point between the yellow and red mark the point of fractal feathering observed in b); b) Arrhenius plot obeying the Fundamental Asymmetry Principle, important in this experiment as the fractal feathering affects are prominent feature of this white mica. The activation energy is calculated using this principle.
One of the important points in this study however is to illustrate that the Arrhenius plots derived from step-heating experiments using white mica can be analysed in a way that is consistent with the FAP (Figure 12). The inferred diffusion parameters produce a retentivity that is not greatly dissimilar to that obtained from high-pressure experiments (Harrison et al. 2009). The activation energy from this study was higher (70.7 kcal/mol) but this is in part compensated for by the values for the normalised frequency factor (D0/r2). Having accomplished this step, it is then possible to derive an r/r0 plot following methods set out by Lovera et al. (1997). Two distinct domain sizes can be recognised with fractal feathering of related size-volume distributions occurring for both domains (Figure 13). The two domains are different in size by about a factor of two and the pattern of gas release theoretically consistent with fractal feathering of the smaller domain size can be readily observed in the apparent age spectrum (Figure 13).
Figure 13. r/r0 plot
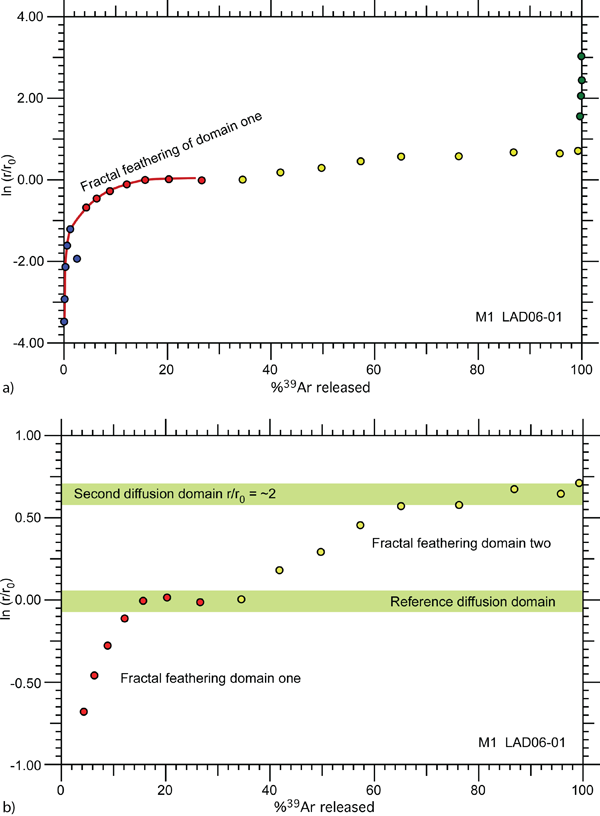
a) An r/r0 plot where points form a relatively flat line (see green bands) it marks distinct domain sizes; a rise to an asymptote in the blue then the red steps represent a domain, repeated with the yellow points; an almost perfect example of what should be expected for fractal feathering; b) same as previous slide except larger scale, the blue green steps omitted. At this scale it is more distinct that two distinct domain sizes in the r/r0 plot occur. Importantly one domain, with the older ages, is twice as thick as the other; both have fractal feathering.