Consistency of Scaling

When scaling analogue experiments, priorities have to be set, because scaling of all possible properties is not possible. In the experiments presented here, there are four free parameters:

• convergence rate,
• surface temperature,
• base temperature and
• initial length.

The initial height of the model (thickness of the lithosphere) does not influence the scaling and is therefore omitted here.

Once a material or a set of materials has been chosen, four material properties are important:

• thermal diffusivity,
• density,
• viscosity and
• activation energy.

Equations 2.2, 2.3, 2.6 and 2.12 couple the eight scales for length, time, viscosity, density, gravity, thermal diffusivity, activation energy and temperature. Furthermore, the Arrhenius Equation

(2.16)

where η₀ is the viscosity at a chosen temperature T₀, couples the material properties viscosity and activation energy.

In the experiments presented here, the scaling factors were determined by following the steps given in Table 3. A summary of the resulting scaling factors for the properties discussed above can be found in Table 4. Having chosen a material, the thermal diffusivity is given and the corresponding scaling factor is fixed. The limitations of the deformation apparatus set the velocity scale. From these two, the length and time scales were calculated. After that, limits for length of the natural scenarios to be modelled could be estimated from the possible initial lengths in the laboratory.

Table 3. Scaling thermomechanical experiments. Given or desired parameters are shown in the top row. From these, various scale factors and properties can be calculated (bottom row) and checked against each other (see text).

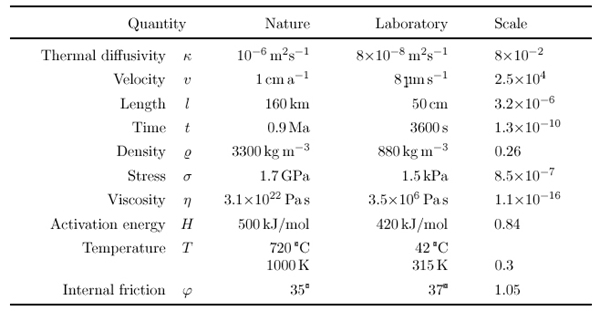Table 4. Scaling factors for the experiments described. The numbers are calculated according to Table 3. Density is given for the ductile materials. For the brittle materials, density is scaled by the same factor. The stresses given are lithostatic stresses at the model base and at the corresponding depth in nature. The value for viscosity was calculated for the top of the upper mantle using parameters for a wet dunite given by Carter & Tsenn (1987). Effective scaling factors for viscosity can differ by some orders of magnitude, depending on material parameters and chosen depth, as is shown in Table 2.

Since the density scale was set by the choice of materials, the scales for stress and viscosity were also given. From the viscosities in nature, those to be used in the laboratory can be calculated, thus determining the temperatures to be used in the experiments.

On the other hand, equation 2.12 couples the temperature scale to the scale for the activation energy, a material property. This relationship overdetermines the problem by adding a further restriction. In the case of the experiments presented here, the absolute value of temperature is the only property being scaled inconsistent with the other properties: The scaling of temperature is off by a factor of two.

Parameters Not Scaled

In analogue models, not all parameters can be scaled. In contrast to the properties consistently scaled, other parameters were not considered in the experiments described in this work. Of some, it can be safely assumed that they do not influence the system on the time-scale or length-scale modelled, such as solar radiation: diurnal surface temperature variations fall to 1% at 1.5m depth, annual variations at 25 m, both lengths being below the resolution for the scaling of length.

Further thermal parameters such as conductivity or heat flux (equation 4.1) concern thermal energies. Since the experiments were performed at temperatures above the phase transition temperature of paraffin waxes of around 26°C (Mancktelow, 1988), effects of thermal energies can be neglected. In addition to these thermal properties, other relationships such as those given in Table 1 can be found, overdetermining the problem even further. Some of these equations are trivial (e. g. equations 4.3 or 4.4). Others describe relationships which are irrelevant to the modelled scenario. For example, elastic properties described by equation 4.5 can be neglected due to the low strain rates.

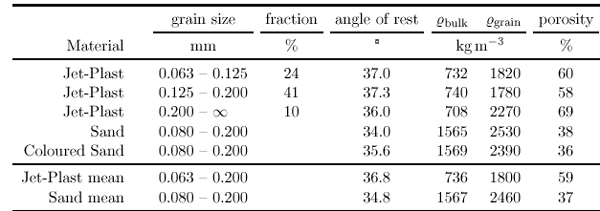Table 5. Properties of brittle materials used. The plastic powder was sieved before analysis, the remaining 25% had a grain size smaller than 0.063mm and were not used. The angle of internal friction was determined measuring the angle of rest of small piles of the material (±2ß). The densities (±8 kg m-3 and the porosity (±2%) were obtained using standard techniques.

Other parameters do influence the system, but cannot be scaled; in fact they cannot be modelled. Sedimentation (e. g. Cobbold et al., 1989; Vendeville & Cobbold, 1988; Sans & Koyi, 2001) and erosion (e. g. Davy & Cobbold, 1991) have been used in analogue modelling. These experiments were done episodically: the deformation was stopped to perform the sedimentation. In the models presented here, the scaling of time prohibited to stop the experiments for sedimentation or erosion: the heat flux could not be stopped. Furthermore, the thermal insulation around the model would have to be disturbed strongly. Nevertheless, numerical models suggest that erosion and sedimentation significantly influence the deformation and its localisation during orogenesis (e. g. Willett et al., 1993; Jamieson et al., 1996).