Analogue modelling of segregation and ascent of magma
Analogue experiments of magma ascent
Magma ascent experiments were performed in a similar tank to the one shown in Figure 1, but measuring 100 x 100 x 0.8 cm. The tank was filled 40 cm deep with gelatine, which is an elastic-brittle material with a Young's modulus of about 103 Pa, a Poisson's ratio of 0.5 and a tensional strength of about 102 Pa (Takada 1990). Instead of producing gas in the sample by fermentation, air was pumped into the gelatine through one of up to six tubes with upwards pointing syringe needles fixed to the ends. A thin wire was inserted in some of the needles and suspended vertically to avoid clogging of the needle during settling of the gelatine and to induce a straight vertical ascent path for the air.
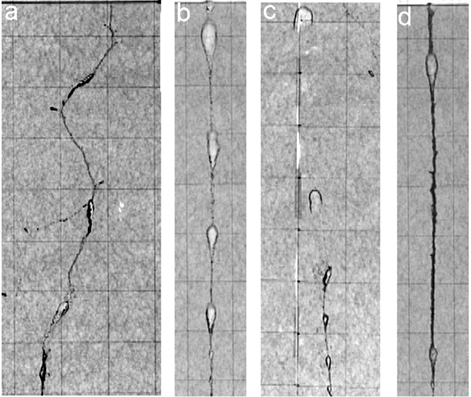
Figure 6 shows the ascent of series of air lenses along a path created by the first ascending air lenses (Fig. 7). Although air flow from the syringe at the bottom was constant, air first accumulated to reach a critical size for ascent (Weertman 1971, Secor & Pollard 1975, Dahm 2000). The ascending air lenses are hydrofractures that move with their content and have been termed "mobile hydrofractures" by Bons (2001), to separate them from the dyke-type hydrofractures that only propagate at their upper tip, but do not close at their rear end. The air-filled mobile hydrofractures have a roughly constant shape and velocity. Obstacles along the path can stop or slow down ascending batches, which leads to accumulation of air batches (Figure 6.c&d). Arrested batches can become mobile again when enough batches have accumulated to overcome the obstacle. Large mobile hydrofractures move faster than small ones (cf. Dahm 2000).
|
Figure 6. Movies of ascending air lens trains along pre-existing fractures, formed by earlier ascending lenses. (a) Regular ascent. Time between frames 0.2 s. (b) Regular ascent along vertical fracture, enforced with wire that was connected to syringe during stiffening of the gelatine and then pulled out. Some accumulation due to variations in lens size and speed occurs. Time between frames 0.04 s. (c) Accumulation at obstacle. Small lenses ascend to an obstacle, where they get halted. Only when enough have accumulated, can the air proceed upwards again, now in a fracture parallel to the glass plate. Also note the shedding of air by imperfect closure and the incorporation of shed air in the next passing lens. Time between frames 0.08 s. (d) Another example of accumulation lenses that accumulate due to variable ascent speeds. Time between frames 0.04 s. Grid spacing is 5 cm. |
|
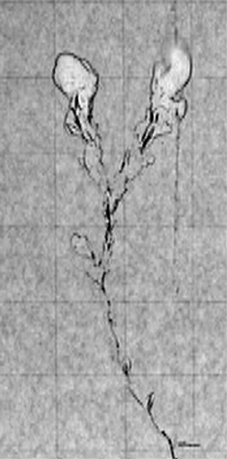
| Figure7. Propagation of initial hydrofracture in unfractured gelatine in 0.8 cm wide glass tank. Air is slowly pumped in from a syringe that is located at the bottom of the image. The fracture is mostly parallel to the glass plates (plane of view). Notice the far-field elastic deformation which can be seen by the offset of a trace of small bubbles to the right of the fracture. Grid spacing is 5 cm; time between frames 0.08 s. |
Both types of experiment show one common characteristic: both movement and accumulation is stepwise and in batches. In the fermentation experiments, gas is produced on the smallest microscopic scale and accumulates in small bubbles and hydrofractures. These in turn occasionally collapse and migrate to merge with others in ever larger volumes, until escape is achieved. The second type of experiment can be regarded to follow from this stage. Batches that escaped from the source area (partial melt) make their way up as mobile hydrofractures. Here the stepwise accumulation of batches continues by two processes: (1) larger and faster batches catch up and merge with smaller and slower ones and (2) obstacles slow down or arrest ascending batches until enough have accumulated to pass the site of high propagation resistance. This stepwise ascent and accumulation is similar to that proposed by Maaløe (1987) and Sleep (1988) from analogue experiments and theoretical modelling.
An interesting observation of both types of experiments is that transport occurs without full connectivity of the mobile phase. Connectivity is only transient and local in the segregation experiments. This is in contrast to models of melt segregation that envisage flow through an interconnected network of pores or fractures (e.g. Nicolas 1986, Collins & Sawyer 1996, Brown & Solar 1998, Weinberg 1999). In that case, the Darcian equation of flow is valid, where flux is proportional to permeability and the gradient in hydraulic head. However, the permeability is zero most of the time in our experiments and flow cannot be described by Darcian flow. The concept of a "critical melt fraction" (van der Molen & Paterson 1979, Vigneresse et al. 1996), the melt fraction at which connectivity is reached and Darcian flow is possible, becomes irrelevant if transport can occur without connectivity.
Some comments on the validity of the experiments
Analogue experiments
such as presented here, should always be scrutinised for their validity.
This paper deals with a type of behaviour, stepwise accumulation and transport
in hydrofractures, that is illustrated, but not proven by the experiments.
The question of the validity of these experiments thus hinges on the question
whether these experiments replicate the behaviour that one may expect
to occur in nature. The behaviour that is observed in the experiments
presented here arises from:
-
The formation of hydrofractures, which are fractures that form by the
internal fluid pressure, rather than by an external tectonic stress (Secor
1965).
- The ability of hydrofractures to propagate when the stress state at
the fracture tip exceeds the resistance to fracturing. Fracture propagation
at a tip can be in both directions: extension of the crack or closure;
- A higher transport rate by stepwise propagation and accumulation of
hydrofractures than by other transport means, such as pervasive flow through
pores or fracture networks.
The actual rheological properties of the matrix phase appear to play at the most a minor role, as experiments with Mohr-Coulomb wet sand (Fig. 2-4) and elastic-brittle stiff gelatine (Fig. 5) yield the same results. We will now address each of the three points mentioned above separately.
Hydrofracturing
The possibility of forming extensional fractures at high confining pressures has been generally accepted, since the concept of effective pressure was introduced by e.g. Sibson et al. (1975). The effective pressure is the lithostatic pressure minus the fluid pressure. Extensional fractures may occur at any depth in the crust or mantle if the effective pressure exceeds the tensile strength of the rock (Sibson et al. 1975; Secor 1965). Evidence for hydrofracturing in deep rocks has been found in the field (e.g. Nicolas & Jackson 1982; Brown et al. 1995) and in experiments on partial melting (e.g. Rushmer 1995). All models on magma transport by dyking are based on the feasibility of creating hydrofractures at depth.
Hydrofracture propagation
The general model of magma ascent in mobile hydrofractures that close at the rear (Weertman 1971, Maaløe 1987, Takada 1990) and the use of air or liquids and gelatine to simulate dykes (Maaløe 1987, Takada 1990, Lister & Kerr 1991, Dahm 2000) has been strongly criticised by, for example, Lister & Kerr (1991) on the grounds that (1) hydrofractures supposedly cannot close at the rear end due to the infinitely high stress needed to squeeze out all fluid from between two parallel plates, and (2) the propagation velocity of dykes is determined by the viscous drag along the dyke, not by fracture toughness as is supposedly the case in the gelatine experiments. Dahm (2000), on the other hand, argues that viscous forces in the rear end of a tear-drop shaped propagating hydrofracture are in fact ascent rate controlling, not the fracture toughness, even in ascending air-filled hydrofractures in gelatine. The flow in the air-filled hydrofractures is laminar, but close to turbulent (Reynold's number ┼ 100 to 1000), as is envisaged for ascending magma in dykes (Emerman et al. 1986, Bruce & Huppert 1990). Dahm (2000) pointed out that most of the rate-controlling viscous pressure drop along the hydrofracture occurs in the very narrow (Ám's) tail (point 2), where minute amounts of air may be left behind, due to imperfect closure (point 1). More importantly, ascent rate is also controlled by irregularities in the fracture surface. The resistance to propagation clearly plays a role here and would in nature if fractures are not as ideal as most mathematical models envisage them to be.
Transport in hydrofractures instead of other transport mechanisms
Although it is accepted that hydrofractures and hydrofracture propagation can occur under geological conditions (see above), surprisingly little research has been done to determine under which conditions transport through or with hydrofractures can compete with other transport mechanisms. Most models on dyke ascent (propagating hydrofractures), explicitly or implicetly assume sufficient influx of magma into the base of the dyke (e.g. MŽriaux & Jaupart 1998). The validity of this assumption or boundary condition, in case of a partially molten rock, has not been investigated in detail, but was challenged by Weinberg (1999) and Bons et al. (2001). In one of the few modelling studies that allow both hydrofracturing and porous flow, Miller and Nur (2000) showed that hydrofracturing is initiated and becomes the dominant transport mechanism for fluid transport through the crust under normal geological conditions. Other indicators for the occurrence of stepwise transport by hydrofractures, other than dykes that may have inititiated from magma chambers, are listed in Bons and van Milligen (2001). Concluding, it appears realistic to assume that transport through hydrofractures may become the dominant transport mechanism for melt.
From the above, it is clear that our experiments are valid attempts to replicate and give insight into the complicated way a melt proceeds from the minute pockets on grain boundaries to large accumulations, such as dykes, sills and batholiths. Our experiments do not replicate dykes as modelled numerically by e.g. Lister and Kerr (1991), as this cannot be done in the equipment that was used, nor was it intended. The experiments are, however, compatible with such dyke models, if one envisages these dykes to be large end-members of stepwise accumulation. Also, we suggest accumulation in ever larger volumes, i.e. magma chambers. Large magma chambers can be drained by dykes, as a large reservoir of magma is available to feed the emerging dyke. The experiments are not compatible with the pervasive melt flow through fracture networks (cf. Weinberg 1999). The reason is that Weinberg (1999) assumes that hydrofractures remain open once they are formed. There are no data on how well and how quickly a fracture can close. In the light of this paper, and those by Bons and van Milligen (2001) and Miller and Nur (2000), it seems that this is an important issue for further research.
Lister and Kerr (1991) presented hydrofracturing experiments with gelatine, but concluded that they are in the wrong physical regime. We do agree that their experiment was in the wrong physical regime to simulate the type of dyke they discussed, or the type of hydrofracture propagation we present here.
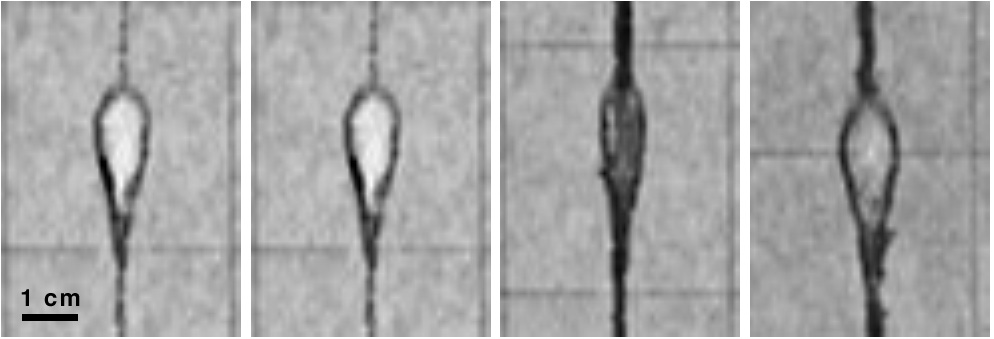
Their liquid-filled hydrofracture was not long enough to close at the rear end to enable a viscous pressure drop to be rate controlling and the glycerol-liquid used, in combination with very slow propagation (10-4 m/s), may have softened the gelatine to give it a high effective resistance to fracture propagation. It should be noted that the fracture tip in the experiment of Lister & Kerr (1991, Fig 7) was blunt, while ascending hydrofractures in our experiments had pointed tips (Fig 8), as envisaged by Rubin (1995b) and Dahm (2000) and indicative of low resistance to fracturing (Lister & Kerr 1991).
|
Figure 8. Close-ups of individual ascending air lenses, showing their tear shape with a narrow tail, as modelled by Dahm (2000). Left two images are from fig 6b, right two from fig. 6d. |
|
 |
Finally, the volume change in the fermentation experiments is unrealistically high. However, the advantage of this is that the process can be studied in its extreme form and for a prolonged period. It should also be taken into account that the effective volume change for any part of a partial melt system can be far more than only caused by local partial melting, if melt is added from other parts of the system. Analogue experiments are never perfect in all aspects, but we think that the fermentation experiments can give valuable insight in the processes that might occur in partial melt systems.
Conclusions
Our analogue experiments on magma accumulation and ascent suggest that both are part of a continuous chain of stepwise movement and mergers of hydrofractures. The process is highly dynamic and non-linear, with periods of quiescence interspersed by sudden bursts of transport and accumulation. Transport occurs before full percolation of the melt phase is reached. Popular concepts, such as steady-state Darcian melt flow and a critical melt fraction appear to be inappropriate to describe such a system.
Experiments were carried out in the Epsilon Laboratory, Monash University, and the Tectonophysics Analogue Laboratory at Mainz University. Elena Druguet, Mark Jessell and Cees Passchier are thanked for their help and support. Part of the project was funded through a Monash University Logan Fellowship to Bons. Win Means is thanked for his constructive review.
References
Anma, R. & Sokoutis, D. 1997. Experimental pluton shapes and tracks above subduction zones. In: Bouchez et al. (eds) Granites: From segregation of melt to emplacement fabrics. 319-334.
Bons, P.D. 2001. The formation of large quartz veins by rapid ascent of fluids in mobile hydrofractures. Tectonophysics, 336, 1-17.
Bons, P.D., Dougherty-Page, J. & Elburg, M.A. 2001 Stepwise accumulation and ascent of magmas. Journal of Metamorphic Geology 19 (in press).
Bons, P.D., van Milligen, B.P. 2001. A new experiment to model self-organized critical transport and accumulation of melt and hydrocarbons from their source rocks. Geology 29 (in press - excpected publication: October)
Brown, M., Averkin, Y.A., McLellan, E.L. and Sawyer, E.W. 1995. Melt segregation in migmatites. Journal of Geophysical Research 100, 15655-15679.
Brown, M. & Solar, G.S. 1998. Shear-zone systems and melts: feedback and self-organization in orogenic belts. Journal of Structural Geology 20, 211-227.
Bruce, P.M. & Huppert, H.E. 1990. Solidification and melting along dykes by the laminar flow of basaltic magma. In: Ryan, M.P. (ed.) Magma Transport and Storage, 87-101.
Clemens, J.D. & Mawer, C.K. 1992. Granitic magma transport by fracture propagation. Tectonophysics, 204, 339-360.
Collins, W.J. & Sawyer, E.W. 1996. Pervasive granitoid magma transfer through the lower-middle crust during non-coaxial compressional deformation. Journal of Metamorphic Geology 14, 565-579.
Dahm, T. 2000. On the shape and velocity of fluid-filled fractures in the earth. Geophysical Journal International 142, 181-192.
Dell'Angelo, L.N. & Tullis, J. 1988. Experimental deformation of partially melted granitic aggregates. Journal of Metamorphic Geology 6, 495-515.
Emerman, S.H., Turcotte, D.L. & Spence, D.A. 1986. Transport of magma and hydrothermal solutions by laminar and turbulent fluid fracture. Physics of the Earth and Planetary Interiors 41, 249-259.
Emerman, S.H. & Marrett, R. 1990. Why dykes? Geology 18, 231-233.
Grujic, D. & Mancktelow, N.S. 1998. Melt-bearing shear zones: analogue experiments and comparison with examples from southern Madagascar. Journal of Structural Geology 20, 673-680.
Hubbert, M.K. & Willis, D.G. 1957. Mechanics of hydraulic fracturing. Trans. Am. Inst. Mech. Engrs. 210, 153-168.
Lister, J.R. & Kerr, R.C. 1991. Fluid-mechanical models of crack-propagation and their application to magma transport in dykes. Journal of Geophysical Research 96, 10049-10077.
Maaløe, S. 1987. The generation and shape of feeder dykes from mantle sources. Contributions to Mineralogy and Petrology 96, 47-55.
McLellan, E.L. 1988. Migmatite structures in the Central Gneiss Complex, Boca de Quadra, Alaska. Journal of Metamorphic Geology 6, 517-542.
Means, W.D. & Park, Y. 1994. New experimental approach to understanding igneous texture. Geology 22, 323-326.
Mériaux, C. & Jaupart, C. 1998. Dike propagation through an elastic plate. Journal of Geophysical Research 103, 18295-18314.
Miller, S.A., & Nur, A., 2000, Permeability as a toggle switch in fluid-controlled crustal processes. Earth and Planetary Science Letters 183, 133-146.
Nicolas, A. 1986. A melt extraction model based on structural studies in mantle peridotites. Journal of Petrology 27, 999-1022.
Nicolas, A. & Jackson, M. 1982. High temperature dikes in peridotites: origin by hydraulic fracturing. Journal of Petrology 23, 568-582.
Park, Y. & Means, W.D. 1996. Direct observation of deformation processes in crystal mushes. Journal of Structural Geology 18, 847-858.
Petford, N., Kerr, R.C. & Lister, J.R. 1993. Dike transport of granitoid magmas. Geology 21, 845-848.
Petford, N., Cruden, A.R., McCaffrey, K.J.W., & Vigneresse, J.-L. 2000. Granite magma formation, transport and emplacement in the Earth's crust. Nature 408, 669-673.
Ramberg, H. 1967. Gravity, Deformation and the Earth's Crust.
Rosenberg, C.L. & Handy, M.R. 2000. Synthectonic melt pathways during simple shearing of a partially molten rock analogue (norcamphor-benzamide). Journal of Geophysical Research 105, 3135-3149.
Rubin, A.M. 1993. Dikes vs. diapirs in viscoelastic rock. Earth and Planetary Science Letters 117, 653-670.
Rubin, A.M. 1995a. Getting granite dykes out of the source region. Journal of Geophysical Research 100, 5911-5929.
Rubin, A.M. 1995b. Why geologists should avoid using 'fracture toughness' (at least for dykes). In: (Baer & Heinmann, eds.) Physics and Chemistry of Dykes. Balkema Rotterdam, pp. 53-63.
Rubin, A.M. 1998. Dike ascent in partially molten rock. Journal of Geophysical Research 103, 20901-20919.
Rushmer, T. 1995. An experimental deformation study of partially molten amphibolite: Application to low-melt fraction segregation. Journal of Geophysical Research 100, 15681-15695.
Secor, D.T. 1965. Role of fluid pressure in jointing. American Journal of Science 263, 633-646.
Secor, D. T. & Pollard, D. D. 1975. On the stability of open hydraulic fractures in the Earth’s crust. Geophysical Research Letters 2, 510-513.
Sibson R H, Moore R M & Rankin A H 1975. Seismic pumping - a hydrothermal transport mechanism. Journal of the Geological Society, London 131, 653-659.
Sleep, N.H. 1988. Tapping of melt by veins and dikes. Journal of Geophysical Research 93, 10,255-10,272.
Spence, D.A. & Turcotte, D.L. 1985. Magma-driven propagation of cracks. Journal of Geophysical Research 90, 575-580.
Takada, A. 1990. Experimental study on propagation of liquid-filled crack in gelatin: shape and velocity in hydrostatic stress condition. Journal of Geophysical Research 95, 8471-8481.
van der Molen, I. & Paterson, M.S. 1979. Experimental deformation of partially melted granite. Contributions to Mineralogy and Petrology 70, 299-318.
Vigneresse, J.-L., Barbey, P. & Cuney, M. 1996. Rheological transitions during partial melting and crystallisation with application to felsic magma segregation and transfer. Journal of Petrology 37, 1579-1600.
Weertman, J. 1971. Theory of water-filled crevasses in glaciers applied to vertical magma transport beneath ocean ridges. Journal of Geophysical Research 76, 1171-1183.
Weinberg, R.F. 1999. Mesoscale pervasive felsic magma migration: alternatives to dyking, Lithos 46, 393-410.
Whitehead, J.A. & Helfrich, R. 1990. Magma waves and diapiric dynamics. In Ryan, M. P. (ed), Magma transport and Storage. 53-76.